Spieltheorie aus VWL Sicht; Einstieg
Info für Kuratoren:
Doppelpost aus Interesse an Aktivität. Ursprünglich auf Hive erschienen (hier).
Doppelpost bleibt eine Ausnahme. Von nun an wahrscheinlich hauptsächlich auf Hive aktiv.
Mehr dazu ganz unten im Artikel.
Dies ist der zweite Artikel meiner Vwl Einstiegs Serie. Teil 1 Einstieg in die Vwl; Märkte findet ihr hier.
Marktformen mit mehr als einem Anbieter
In Märkten mit nur einem Anbieter (Monopol) ist die Preisgestaltung sehr einfach, da der Monopolist eben diese exakt auf die Marktbedingungen anpassen kann und so den optimalen Gewinn einfahren kann.
Komplizierter wird diese Preisgestaltung in Märkten mit zwei ähnlich großen Wettbewerbern (Duopol).
Es gibt auch noch Märkte mit über zwei Anbietern aber dennoch nicht so vielen aktiven (Oligopol) und Märkte mit sehr vielen Anbietern (Polypol).1
Schon in einem Duopol, also mit nur einem Konkurrent, muss jeder Anbieter damit rechnen, dass die eigene Preissetzung durch den Wettbewerber unterlaufen wird.
Diese „strategische Interdependenz“ kann mit mehreren Modellen beschrieben werden, von denen ich mich hier auf das sogenannte „Cournot-Modell“ beschränken werde.1
Cournot-Modell
Dieses Modell eines Marktes mit zwei Anbietern (Duopol) geht davon aus, dass beide Anbieter gleichberechtigt sind und ihre Preisgestaltung gleichzeitig machen müssen. Jeder der beiden versucht natürlich eine Strategie zu entwickeln mit der er einen optimalen Absatz erreichen kann, wofür er das Verhalten seines Konkurrenten vorwegnimmt (antizipiert). Begonnen wird dies mit der Reaktionsfunktion, die auf den Überlegungen eines Anbieters A basiert, der sich fragt, welche Menge er anbieten soll (optimale Absatzmenge xA), bei einer antizipierten Angebotsmenge seines Konkurrenten B.
Die Reaktionsfunktion lautet:
xA=a/2b – xB/2 – 1/2b
Wobei a als Prohibitivpreis und x als menge definiert sind. (Preis wäre: a-bx).
Die für Anbieter A optimale Strategie hängt also unmittelbar von der Strategie von Anbieter B ab. 1
Die Reaktionsfunktionen von zwei Anbietern lassen sich grafisch wie folgt abbilden:

Der Schnittpunkt der beiden Reaktionsfunktionen, der selbstverständlich auch rechnerisch bestimmbar ist (gleichsetzen von xa und xb), wird als sogenanntes „Nash-Gleichgewicht“ bezeichnet, indem die beiden Akteure das Ergebnis für sich optimal wählen und dabei berücksichtigen, dass der Konkurrent sich nach der gleichen Strategie verhält1.
Das Gefangenendilemma
Das Gefangenendilemma ist die bekannteste Interaktion von zwei Parteien in der Spieltheorie.
Das Szenario ist das folgende:1
Zwei Verbrecher wurden mit gestohlenen Gütern gefasst und werden getrennt voneinander verhört. Ihnen wird ein Einbruch vorgeworfen. Sie haben nun drei Möglichkeiten:
Wenn sie beide nicht gestehen, kann ihnen der Einbruch nicht nachgewiesen werden und sie bekommen beide nur eine 6 monatige Haftstrafe aufgrund der gestohlenen Güter.
Wenn beide den Einbruch gestehen, werden sie zu jeweils 2 jahren Haft verurteilt.
Gesteht nur einer der beiden den Einbruch, wird er als Kronzeuge freigelassen. Sein Partner bekommt dann allerdings eine Haftstrafe von 5 Jahren.
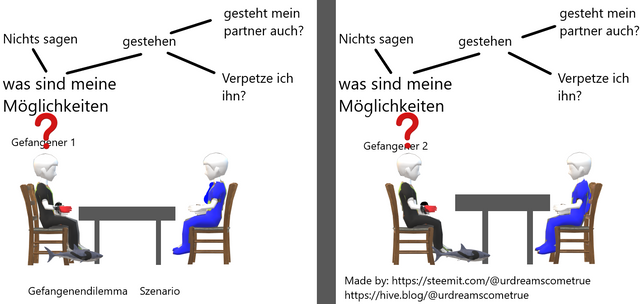
Wie sollten sich die beiden Gefangenen also idealerweise entscheiden?
Gefangener 1 und Gefangener 2 haben jeweils zwei Möglichkeiten, sie können jeweils das verbrechen abstreiten oder gestehen. Somit sind bei diesem Szenario vier Ergebnisse möglich, die in einer Auszahlungsmatrix dargestellt werden können.
Für „Gefangenen 1“ wäre es, wenn „Gefangener 2“ gesteht, das beste ebenfalls gestehen. Wenn Gefangener 2 nicht gesteht, ist es für Gefangenen 1 immernoch besser zu gestehen, da er dann ohne Haftstrafe davonkommt. Für den Gefangenen1 ist somit gestehen die dominante Strategie. Da für gefangenen 2 die gleiche Entscheidungsstruktur gilt, ergibt sich als Lösung, das beide gestehen.
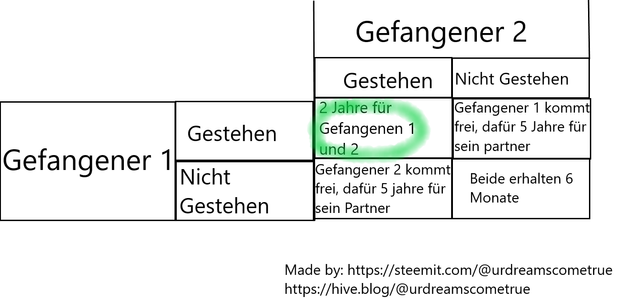
Wie man sieht führt das Gefangenen Dilemma zu einer Art Rationalitätenfalle, da das individuell rationale verhalten der beiden zu einem ungünstigen Ergebnis führt (2 jahre Gefängnis, statt 6 Monate für beide).
Die wichtigsten Voraussetzungen eines „Gefangenen-Dilemmas“, sind also die Unmöglichkeit einer Kommunikation zwischen den beiden Akteuren. Dies erklärt sich dadurch, dass sich die beiden durch eine ermöglichte Kommunikation miteinander darauf absprechen könnten dichtzuhalten und nichts zu verraten, was die geringste Strafe für beide garantieren würde.
Außerdem ist es wichtig, dass das Spiel nicht wiederholt wird, da sonst eine Reputation der Akteure entsteht, die das Ergebnis beeinflusst (ist Gefangener 1 als Verräter bekannt oder als loyal... verändert sich das Dilemma komplett).
Die komplizierte Entscheidungssituation der beiden Anbieter des Duopol Marktes kann man nun also grundsätzlich in das Schema des Gefangenendilemmas übertragen.
In diesem Beispiel würden also auch 4 Ergebnisse resultieren, aus den Möglichkeiten der beiden Anbieter entweder die zum monopol passende Menge (Grenzkosten=Grenzerlöse) anzubieten (funktioniert nur gut, wenn der Konkurrent sich ebenso verhält) oder die Menge die sich aus der Reaktionsfunktion des Cournot Modells ergibt.
Auch hier sieht man schnell wieder, dass die Standard Lösung des Gefangenen Dilemmas nicht zur für beide optimalen Lösung führt.
Dies lässt sich so schnell erkennen, da die Cournot Lösung ihrer logischen Struktur nach, darauf abzielt die beste Lösung bei gegebenem Konkurrenz Verhalten zu erzielen.
Demnach ist es für die beiden Konkurrenten immer besser die Cournot Lösung zu wählen, egal was der Konkurrent wählt, da sie so eine höhere rente erwirtschaften können.
Die für beide optimalste Lösung eines gemeinschaftlichen Monopols würde im gefangenen dilemma also nicht zustande kommen.
Dieses Beispiel ist allerdings sehr konstruiert, da es ein einmaliges Spiel ist und keine Kommunikation stattfindet.
Bei einem wiederholten Gefangenen Dilemma Spiel wäre eine „wie du mir, so ich dir“ Strategie nach Robert Axelrod (1984) am erfolgreichsten, bei der man sich im ersten zug kooperativ verhält und dann sein Verhalten dem seines Konkurrenten anpasst.
Das war es mit meinem zweiten Vwl Artikel, Fortsetzungen werden vermutlich folgen. (Unsicherheit bei Hive und steem kommt mir derzeit groß vor). Sollte ich meine artikel woanders veröffentlichen, werde ich sowohl auf steem als auf Hive darüber informieren.
Die Artikel gehen je nach Bereich und meiner Einschätzung mehr oder weniger in die Tiefe und sollen nur für ein Grundlegendes Verständnis sorgen, für ein tiefes Verständnis muss man selbstverständlich weitere Recherchen durchführen.
Da es mir um Verständnis geht, werde ich auch in Zukunft höchstens am Rande auf mathematische Bestimmungen eingehen und eher versuchen die Fragen durch eine logische Argumentation zu beantworten um die im Verhältnis stehenden Ursachen einer Veränderung oä. Zu klären.
Quelle 1 : "Grundzüge der Volkswirtschaftslehre" "Eine Einführung in die Wissenschaft von Märkten" von Peter Bofinger
Weiterführende Literatur: https://core-econ.org/the-economy/book/text/0-3-contents.html
Abbildungen selbst mit Paint3D erstellt.
Kurzes Satement zu Hive
Wie oben erwähnt fokussiert sich meine Posting Aktivität wohl auf Hive und da ich ungern alles doppelt posten möchte (auch aus moralischen gründe, klar jeder darf seinen Content merhmals verwenden aber zu excessiv betrieben schadet das denke ich der Plattform und hat dann auch keinen Sinn mehr), bedeutet das wohl, dass es hier post technisch sehr ruhig wird.
Sporadisch Kuratieren werde ich weiterhin, auch wenn ich einen Powerdown eingeleitet habe(auf beiden Chains, weil die aktuelle Lage mir sehr unsicher erscheint).
Ich will damit nicht sagen, dass ich die "Entstehung von Hive" positiv betrachte, wie ich mehrmals hier zum Ausdruck gebracht habe, hätte ich mir eine andere Vorangehensweise bei den Problemen mit Sun, sowie dem Ninja mined stake gewünscht; ich bin mir sicher man hätte eine friedlichere lösung gefunden, die für alle beteiligten besser gewesen wäre.
Ich habe jedoch den Eindruck, dass die meisten auf Hive aktiver sind. Ich hoffe das viele der "alten Witnesses" dort, die teilweise die Situation mit Justin Sun sehr schlecht bzw unnötig provokativ gelöst haben (was für alle beteiligten die NICHT optimale Lösung wurde) durch andere Community Mitglieder ersetzt werden.
Chancen sehe ich noch auf beiden Chains (Steem und Hive; freut mich Steemchiller hier an der Spitze der Witnesses zu sehen, eine gute Sache).
Dankeschön, viel Erfolg.