Liebe Steemit Community,
Liebe Freiheitsfreunde,
Liebe Freiheitsfeinde,

sehnsüchtig habe ich auf den Erscheinungstermin des neuesten Werkes von Nassim Taleb gewartet:

Über dieses Buch werde ich noch einen eigenen Artikel schreiben.
Möglicherweise auch eine Artikelserie, da in den Büchern von Nassim Taleb so viel drin steckt, dass es schwierig ist, alles in einem Artikel unter zu bringen.

Kommen wir erst einmal zur Person Nassim Taleb:

Nassim Nicholas Taleb, PhD

(Bildquelle: Wikipedia)
Nassim Nicholas Taleb stammt aus dem Libanon, ist aber amerikanischer Staatsbürger.
Er ist, wie ich finde, einer der wenigen Autoren, die man als Universalgelehrten bezeichnen kann.
Nassim Taleb ist Finanzmathematiker, Risikoanalyst, ehemaliger Floor Trader an der CME (Options), Philosoph und Autor.
Im Gegensatz zu vielen anderen Autoren und Gelehrten, ist ihm Political Correctness völlig unbekannt und man kann sagen, dass er definitiv Eier in der Hose hat (anderes hätte er als Floor Trader sowieso nicht überlebt).
Wer einen kleinen Einblick in Nassim Talebs Denkweise und Ansichten bekommen will, ohne seine Bücher zu lesen, sollte ihm auf Twitter folgen:
@nntaleb
Neben Skin in the Game hat er noch folgende Bücher geschrieben:

Ich kann nur jedem empfehlen, alle seine Bücher zu lesen.

Nassim Taleb schreibt in seinen Büchern sehr viel über Finanzmärkte, Derivate, Stock Market Randomness und Black Swans.
Da diese Dinge für Nichttrader etwas schwierig zu verstehen sind, möchte ich euch heute einige Hilfen geben, um Nassim Talebs Bücher besser verstehen zu können.

Nassim Taleb hat als Trader ein Vermögen gemacht, weil er erkannt hat, dass die Optionsmärkte die Risiken eines sogenannten Black Swan Events, also große Börsencrashs, die statistisch gesehen, eigentlich nur sehr selten (oder gar nicht) auftauchen sollten, nicht richtig eingepreist haben.

Der größte Börsencrash in der Geschichte war der 1987- Crash (Black Monday).
An diesem 19. Oktober 1987 verlor der S&P 500 Index über 20%.
Nassim Taleb war zu dieser Zeit Floor Trader und handelte Optionen.
Optionen war zu diesem Zeitpunkt noch relativ neu. Natürlich gibt es Optionen schon seit hunderten von Jahren, aber der Börsenhandel für standardisierte Otionskontrakte begann an der Börse in Chicago (Chicago Board of Options Exchange) erst im Jahr 1973 mit Call Optionen.
Put Optionen und Index Optionen wurden noch später eingeführt.

Wer mehr über Optionen wissen will, kann meine Artikelserie über Optionen lesen:
https://steemit.com/money/@stehaller/introduction-into-option-trading-lesson-1
https://steemit.com/money/@stehaller/introduction-into-option-trading-lesson-2
https://steemit.com/money/@stehaller/introduction-into-options-trading-lesson-3
https://steemit.com/money/@stehaller/introduction-into-options-trading-lesson-4
https://steemit.com/money/@stehaller/introduction-into-options-trading-lesson-5

Leider kann ich diese Artikelserie nicht mehr weiterführen, da ich mich entschlossen habe, gleich ein Buch darüber zu schreiben.

Nun aber zurück zu dem 87 Crash und den Optionen.
Das mathematische Modell für Optionen , das Black-Scholes- Modell von 1973, für das Fischer Black und Myron Samuel Scholes 1997 den Wirtschaftsnobelpreis bekommen haben, geht von einer Gaußschen Normalverteilung aus:

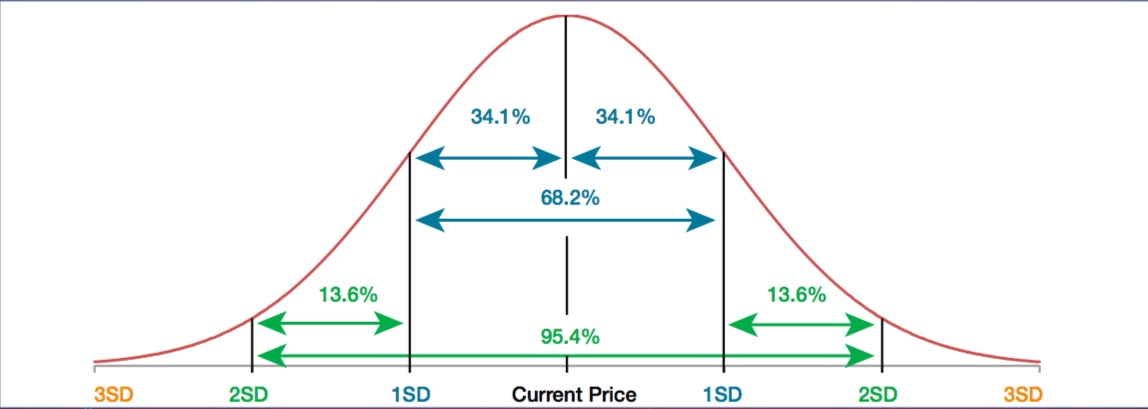
Man geht also bei diesem Modell davon aus, dass sich Aktienpreise komplett “random” verhalten und dass große down moves genauso wahrscheinlich sind und genau so häufig auftreten, wie up moves.
In 68.2% der Fälle bewegen sich die Kurse einer Aktie in einer Schwankungsbreite von 1 Standardabweichung (standard deviation), in 95.4% der Fälle innerhalb von zwei Standardabweichungen und in 99.7% der Fälle bewegen sich die Kurse einer Aktie innerhalb von drei Standardabweichungen.

Wie berechnet man das?
Um die Schwankungsbreite einer Aktie zu berechnen braucht man die Implied Voltaility (erwartete Voltilität) und die Zeit für die man die Schwankungsbreite wissen will. Wenn man Optionen handelt, nimmt man für die Anzahl der Tage einfach die days till expiration (DTE), also die Anzahl der Tage bis die Option verfällt.
Mit folgender Formel kann man dann die Schwankungsbreite berechnen:

(Aktienkurs x IV)/100 x Wurzel aus (DTE/365)

Da es an der Börse heute einigermaßen runter ging, berechnen wir mal die Schwankungsbreite, die der Markt gestern für den heutigen Tag erwartet hat und schauen dann, um wie viele Standardabweichungen sich der Markt tatsächlich bewegt hat.

Wir nehmen als Beispiel den S&P 500 Index (SPX).
SPX Schlusskurs 28.02.2017: 2713.83
Implied Volatility 19.85%

(2713.83 x 19.85)/100 x Wurzel aus (1/365) = 28.20

Der Markt hat also gestern erwartet, dass der SPX heute mit einer Wahrscheinlichkeit von 68% (1 Standardabweichung) innerhalb einer Schwankungsbreite von 28.20 Punkten nach oben und unten schließt.
Also zwischen 2685.63 und 2742.03.
Der SPX hat heute aber 36.16 Punkte niedriger geschlossen.
Er hat außerhalb einer Standardabweichung, aber innerhalb von 2 Standardabweichungen geschlossen.
1.28 Standardabweichungen ,um genau zu sein.

Weil man also bis 1987 davon ausging, dass sich die Kursbewegungen von Aktien einer Normalverteilung angleichen, kosteten Put-Option, mit denen man auf fallende Kurse spekulieren kann, genauso viel wie Call-Optionen, mit denen man auf steigenden Kurse spekuliert.
Angenommen der Kurs einer Aktie war bei $100, dann kostete die Call Option mit Ausübungspreis 105, sagen wir $5 und die Put Option mit Ausübungspreis 95 auch $5.
Dies hat sich als falsch herausgestellt und Nassim Taleb hat das ausgenutzt.
Er hatte offensichtlich die großen Börsencrashs, die es in der Geschichte gab, nicht vergessen.
In der Regel sind Sell-Offs an den Börsen immer viel größer und panischer, als Rallies. Deshalb waren zu der Zeit des 1987-Crahs und auch vorher, Put Optionen zu billig.
Vor allem die Put Optionen deren Ausübungspreis viel tiefer lag, als der aktuelle Aktienkurs.

Nachfolgendes Bild zeigt die tatsächliche Verteilung von Kursbewegungen an der Börse:

(Bildquelle: tastytrade.com)

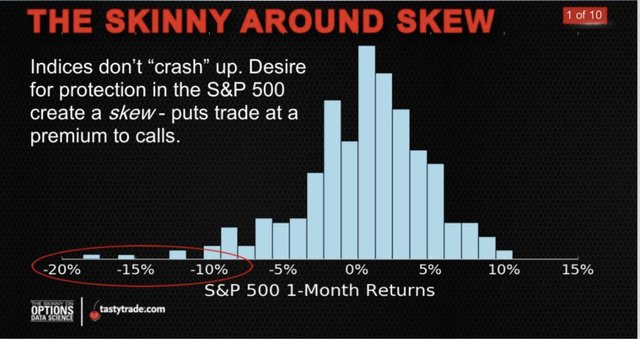
Die Kurse gleichen sich also nicht perfekt einer Normalverteilung an.

Nachfolgendes Bild zeigt in der linken Spalte, wie häufig in der Theorie 1,2,3,4 und 5 Standard Deviation Moves an der Börse auftreten sollten und die rechte Spalte zeigt die tatsächliche Anzahl der jeweiligen Moves:

(Bildquelle: tastytrade.com)

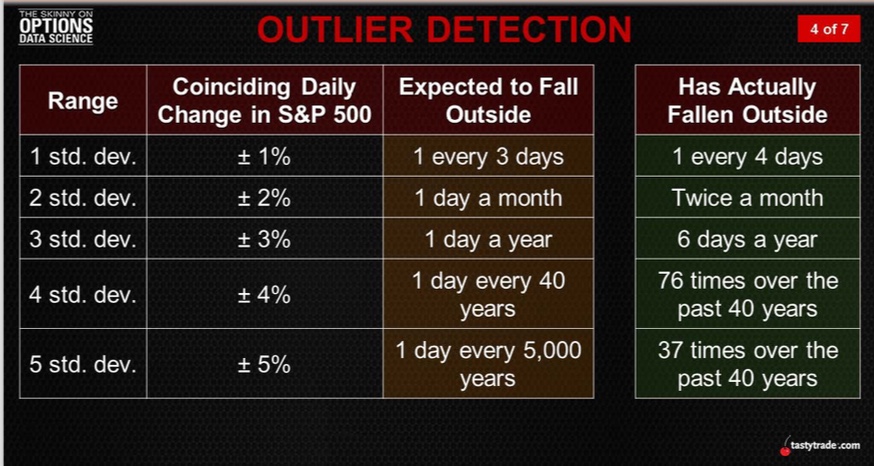
Die Black Swan Events, also 3 Standardabweichungen oder mehr, treten also weit häufiger auf, als die Mathematik voraussagt.

Seit dem Crash von 1987 haben Optionen einen sogenannten Put-Skew, d.h. Put Optionen sind viel teurer, als die entsprechenden Call Optionen.
Die alte Börsenweisheit: ”Markets take the stairs up and the elevator down” drückt sich seit dem Crash von 1987 in den Optionspreisen aus.
Bei unserem Beispiel von oben, wo der Aktienkurs bei $100 war, würde also heute die Put Option mit Ausübungspreis 95, nicht mehr $5 kosten, sondern vielleicht $7 und die Call Option mit Ausübungspreis 105, würde heute nur noch vielleicht $3 kosten und nicht mehr $5.
Oder nehmen mir mal ein reales Beispiel:

S&P 500 ETF (SPY), heutiger Schlusskurs $267.70
April 258 Put: $3.75
April 278 Call: $$1.69

Die Puts, die $10 vom aktuellen Preis entfernt sind, kosten also mehr als doppelt so viel wie die Calls, die $10 vom aktuellen Kurs entfernt sind.

Die Märkte haben sich also seit dem 1987 Crash angepasst, und es dürfte für Nassim Taleb heute nicht mehr so leicht sein, wie 1987.

Ich hoffe, ich konnte Euch mit diesem Artikel etwas helfen, so dass ihr beim Lesen von Nassim Talebs Bücher wirklich alles versteht.

Bis bald,

Stephan Haller

Quellen:
https://en.wikipedia.org/wiki/Nassim_Nicholas_Taleb
http://www.fooledbyrandomness.com
https://en.wikipedia.org/wiki/Black–Scholes_model
https://www.tastytrade.com/tt/