딥알못이 바라본 딥러닝과 그 아이디어
0. 딥러닝은 정말 다른거 같은데 ...
알파고 이후로 딥러닝은 이제 저같은 비전공자들한테도 유명해져서 딥러닝으로 바둑도 하고, 운전도 한다는 소리를 듣고 있으면 정말 앞으론 딥러닝을 아는 사람과 모르는 사람으로 구분되는게 아닐까? 하는 생각이 듭니다.
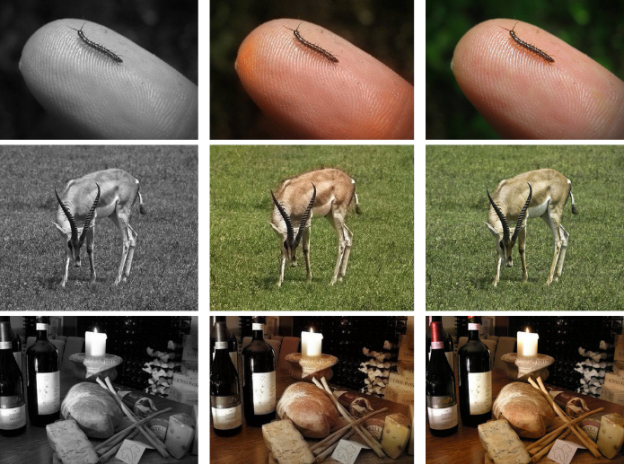
[1. 흑백 사진을 컬러 사진으로 만들어 버리기~ 딥 러닝띠!]
저는 컴퓨터 공학 전공자가 아니지만 딥러닝으로 뭔가를 해보고 싶다는 생각도 있고, 기존 AI와 뭐가 다르기에 저런 빛나는 성과들이 가능할까 궁금했습니다. 혹시 딥러닝이 이해하기 쉬운 거라면, 빨리 배워서 꿀 빨 생각으로 유튜브랑 구글링을 해봤습니다. 그렇게 생소한 기술은 아니더라구요.
1. 딥러닝과 선형회귀
딥러닝을 검색하니 퍼셉트론이 어쩌고 컨볼루션 뉴럴 네트워크가 어쩌고 .. 지도학습이니 비지도학습이니 하는 어려운 이야기가 많지만 딥러닝이란 친구가 어떻게 생긴 친구인지 윤곽을 알려면 회귀(regression)을 아는게 중요한 것 같더라구요.
회귀라는 것은 어떤 데이터들이 막 뿌려져있을때 그 데이터를 표현하는 일종의 방정식을 찾는 과정을 말하는 것 같습니다.
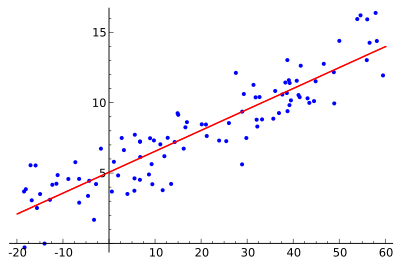
[2. 예측은 언제나 오차가 있음!]
고등학생땐지 중학생땐지 모르겠지만 과거 어느 순간에 배웠던 직선의 방정식은 y = a * x + b 입니다?
그리고 두 점을 안다면, a와 b의 정확한 값도 알아낼 수 있지요?
그러니 점 (1,0)과 점 (0,3)을 지나는 직선이 있다면, 그 직선의 방정식 y = (3-0)/(0-1)*(x-1) + 0 = -3x + 3 입니다?
회귀는 이것과는 좀 다르지만 아무튼 방정식의 a와 b를 찾아가는 과정 입니다. 데이터를 보는 사람들이 회귀를 좋아하는 이유는 데이터 간의 관계를 명확하게 표현할 수 있기 때문이죠.
예를 들어 스팀잇 포스트의 글자 수와 찐다력이 위 그래프와 같은 관계가 있다면, 저는 이 포스트에 500글자가 있으니 찐따력이 대략 303쯤 되겠죠. 그럼 쉽게 '이 친구는 303찐따 구나.' 하고 이야기 할 수 있는 겁니다.
2. 근데 그거랑 딥러닝이랑 뭔 상관?
deep learning. deep은 뭔지 모르겠지만 learning은 뭔가를 배운다는 말이겠죠? 뭘 배울까요?
다시 직선의 방정식으로 돌아가면 y = ax+b 에서 a와 b가 그 직선의 특징을 결정합니다. 기울기는 몇이고 x가 0일 때 y 값은 뭐고 이런 것들요.
컴퓨터가 학습하는 것은 a와 b의 값입니다.
(0,0), (1,2.3), (33,2), (-1,2.3) 이런 값이 있을 때 이걸 가장 잘 표현할 수 있는 a와 b가 뭔지 찾아가는 과정을 회귀라고 하고 딥러닝도 이런 것들 중 하나지요.
그래서 저거랑 개돼지와 사람을 구분하는 문제는 무슨 상관이 있지요?
뭔가가 개돼지인지 사람인지 구분하는 질문의 답은 yes/no 로 나오잖아요? 은혜로운 수학자님들은 그런 yes/no를 표현할 수 있는 함수도 만들었습니다. 바로 sigmoid 함수!
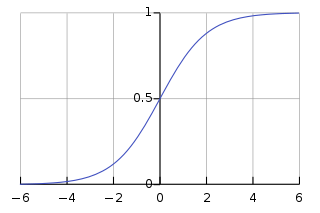
[3. 함수계의 머법관님! 이 포스팅은 고양이가 썼습니다 ㅠ.ㅠ]
위 함수를 보면 S의 양 끝을 잡아당긴 것처럼 생겼는데, 왼쪽은 0, 오른쪽은 1의 값을 가집니다. 그러면 0이면 구라고 1이면 참 이라고 약속 할 수 있겠지요.
그럼 다시, 직선의 방정식에서 a, b를 찾았던 것처럼, 시그모이드 함수의 a, b를 찾으면 시그모이드 함수는 머법관 행세를 무탈하게 할 수 있는 것이지요.
예를들어, 한 포스트에 글을 400자 이상 쓰면 찐따라고 해봅시다. 그런데 제 글은 500자니까 그럼 시그모이드 함수 값은 1에 매우 가깝게 나오게 될 것입니다. -삐빅, 찐따 입니다.
딥러닝은 위와 같은 시그모이드 함수의 계수들을 찾는 과정 입니다. 퍼셉트론이라는 것은 저런 시그모이드 함수가 하나 있다는 것이고 그걸 연결하면 신경망이 되는거지요.
이 포스트에서 딥러닝에 대한 구체적인 얘기는 1도 하지 않았습니다. 하지만 대충 딥러닝이 저런 식으로 작동하는 구나... 정도는 알 수 있겠지요. 어디가서 아는 척 할땐 이 정도로 충분한 것 같습니다.
오류가 있을텐데 많은 지도 편달 부탁 드립니다.
그림 출처
스팀잇에서 머신러닝 글은 잘 못봤는데.
이해가 쉽게 설명해주시는 것 같아요. 잘 보고 갑니다~
오 글이 쉽게 읽히는게 정말인가요? ㅠ.ㅠ 그렇다면 감사합니다!!
제가 생각했던거 보다 딥러닝이 꽤 어렵더군요ㅠㅠ