Ethereum White Paper, Explained. Part 1

In the following blog posts, we will be dissecting the Ethereum white paper by describing it in layman terms. As the paper is too long to fit into one blog post, we will be dividing it into several sections. We will try to explain the niche details mentioned in the Ethereum white paper in the simplest terms possible.
Introduction and Existing concepts
We all know that Satoshi Nakamoto’s development of Bitcoin gave rise to the monumental technology known as — Blockchain. Hopefully, you already know what Blockchain technology is, thanks to our previous posts.
There are numerous other applications for Blockchain technology some of them include: coloured coins, smart property, namecoin, smart contracts or DAO (Decentralised Autonomous Organizations). These applications are complex to build on top of the Bitcoin blockchain. To address this issue, Ethereum proposes a Turing-complete programming language that can be used to create smart contracts or encode complicated functions. A Turing-complete language can essentially be used to simulate a Turing machine. A Turing machine is a model that can simulate any computer algorithm regardless of the complexity.
The Ethereum foundation proposes that all of the above can be achieved effortlessly in a few lines of code. We will validate this claim further in this blog and future posts.
History
Digital currencies as a concept have been prevalent for decades. In the 80s and 90s, a cryptography technique called Chaumian Blinding was used. However, they relied on a centralised intermediary which was a clear deal breaker. Then came B-money which proposed a decentralized consensus system but how that would be achieved was debatable. This was followed by Hal Finney proposing reusable proofs of work which when combined with the concept of B-money seemed promising at first but attempts to implicate such a solution were unsuccessful.
Satoshi Nakamoto collated all of these concepts along with other established primitive technologies for managing ownership through cryptography techniques. The consensus algorithm used by the Bitcoin Blockchain to keep track of the coins is called proof of work.
The proof of work consensus mechanism was a major breakthrough in this area as it solved two main problems.
Nodes in the network could now easily agree on using the consensus algorithm to enter transactions in the distributed ledger.
The problem of who gets to decide the entry into the distributed ledger was solved by using the computing power each node is willing to spend.
For miners, this essentially means — More computing power = More blocks mined = More crypto rewards.
Another concept called proof of stake calculates the weight of a node in the voting process based on the number of coins it holds and not just computational resources.
State transition systems
The ledger of any cryptocurrency is essentially a state transition system which at any given point in time holds information about how many coins are there in individual wallets and the transactions done by these wallets.
In the below diagram there are three main blocks to be considered.
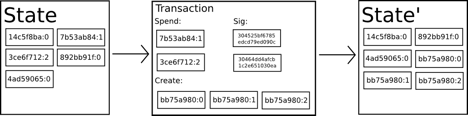
State — This consists of all ownership information contained in the ledger which is cryptographically encrypted.
Transaction — Transaction block defines the amount of the transfer that is initiated in the system. It also includes a signature which is defined by the sender.
State’ — This state consists of the final ownership information that is distributed across all nodes. This State’ will then act as State in the next transaction.
In a traditional fiat banking setting, the states are individual balance sheets and when money is sent from A to B, their individual records get updated.
Obviously, using traditional banks we cannot send more money than we have in our individual accounts, a similar logic has been applied here which is defined by the following function.
APPLY(S,TX) -> S’ or ERROR
To illustrate this in the context of the banking example, we can translate it into the following expression.
CRYPTO
APPLY(S,TX) -> S’
BANKS
APPLY({ Alice: $50, Bob: $50 },”send $20 from Alice to Bob”) = { Alice: $30, Bob: $70 }
Here S is the initial state where both Alice and Bob have $50 in their accounts.
TX is the transaction which defines “send $20 from Alice to Bob”
S’ is the final state which reflects the updated balances of Alice and Bob
Before moving to the next scenario, we must understand how the possession of coins in individual accounts is calculated.
A bitcoin “state” has the collection of all coins that exist along with the public key of their owner. The collection of these coins are determined by total UTXO associated with the address. UTXO is Unspent Transaction Outputs, which as the name suggests have not been spent by the owner. These outputs are measured by checking if the coins that came from the previous owner were also UTXO, to begin with. This is confirmed by checking the previous owner’s UTXO and pairing it with the cryptographic signature produced by the previous owner’s private key.
Now let us analyse what happens if you try selling coins that you don’t have?
CRYPTO
APPLY(S,TX) -> ERROR
BANKS
APPLY({ Alice: $50, Bob: $50 },”send $70 from Alice to Bob”) = ERROR
- Check the value mentioned in TX ($70)
a. If this value is not verified by UTXO of the owner, then it is not present in their account. Return an error.
b. If the mentioned cryptographic signature does not match the signature of the owner, return an error.
If the sum of all UTXO of the owner is less than the figure mentioned in TX, return an error.
If the transaction is valid, transfer funds to the receiver. This transfer happens by removing the input UTXO from the sender and adding it under the receiver’s public key address.
Step 1a prevents the sender from sending coins that do not exist and step 1b prevents senders from sending other people’s coins.
Step 2 makes sure that there are enough coins with the sender before proceeding with the transaction.
Step 3 completes the process by subtracting values from the sender and adding it in the receiver’s wallet.
Now, these steps might look easy to visualize but behind the scenes, there is a lot going on.
The following example should help you better understand.
Suppose you go out to buy a bunch of Bananas. Now for some vague reason, 1 banana costs $75. In a traditional setup, to see if you can afford this precious overpriced banana, you will open your wallet and check the balance. You have two notes of $50 each totalling $100 (50+50=100, duh!). These two notes were given to you by your mom to buy Bananas.
To be able to afford this Banana you have to give away both your $50 notes to the Banana seller and he will return $25 using a combination of USD note denominations. You are now a proud owner of this super expensive Banana. The real problem that now lies ahead of you, is explaining to your mom the price of 1 Banana.
This is reasonably simple to understand, now let us see what happens in a typical cryptocurrency transaction.
Consider Alice wants to send 75 BTC (yes, Alice is filthy rich) to Bob. To proceed she will first check if she has 75 BTC in her wallet. To check this, she must sum up all of her UTXO (value inputs). Consider this UTXO as the two notes of $50 in the previous example. However, Alice has two UTXO values in her wallet of 50 BTC each. This implies that Alice has received two transactions into her wallet. Each UTXO is worth 50 BTC.
Now, we know that you cannot cut a $100 note into two parts to divide into two $50 notes, that would render the $100 note worthless. However, in cryptocurrency, you can do microtransactions by dividing 1 coin into ten 0.1 coins. This division is, however, not straightforward.
To transfer 75 BTC to Bob, Alice will create a transaction with the two 50 BTC inputs to give out two outputs. One output will be given to Bob, another balance will be transferred back into Alice’s wallet.
50BTC + 50BTC → 75BTC to Bob + 25BTC to Alice
In this scenario, Bob is not entrusted with returning the balance as compared to the previous example. Rather the transaction handles the return of the remaining balance output to Alice.
Mining

In an ideal society where we could trust a centralized system with all transactions, this step would be totally unnecessary. But we are trying to create a decentralized consensus system that has the potential to disrupt the monopoly that banks have over our economies. Mining is a method by which we can combine the state transition system with a consensus system such that all nodes in the network agree on the transactions. These transactions are combined and packaged into blocks as shown in the below figure.
The Bitcoin network produces 1 block every 10 minutes. Each block has a timestamp, a nonce (an arbitrary non-repeatable number), a reference to the previous block mentioned as Prevhash in the above diagram and the list of all transactions that have taken place after the previous block is mined. This never-ending chain of blocks always represents the latest state of the distributed ledger and thus acquires its name — the Blockchain.
The following steps check the validity of a block:
Check if the previous block referenced by the block exists and is valid.
Check that the timestamp of the block is greater than that of the previous block and less than 2 hours into the future.
Check that the proof of work on the block is valid.
Let S[0] be the state at the end of the previous block.
Suppose TX is the block’s transaction list with n transactions. For all i in 0…n-1, set S[i+1] = APPLY(S[i],TX[i]) If any application returns an error, exit and return false.
Return true, and register S[n] as the state at the end of this block.
Points 1 to 3 are straightforward. However, the next 3 points might sound a bit confusing. Let us understand how that works.
As mentioned in point 4, let S[0] be the state at the end of Block 5624.
In point 5 it is mentioned that for each n transaction, there is a particular state as follows:
So by the function → S[i+1] = APPLY(S[i],TX[i])
We have the following:
S[1] = APPLY(S[0],TX[0]) ← First transaction
S[2] = APPLY(S[1],TX[1]) ← Second transaction
.
.
S[n] = APPLY(S[n-1],TX[n-1]) ← nth transaction
If you remember the function that we read about in the previous topic. We should be able to backtrack the value of S’ based on the Apply function.
APPLY(S,TX) -> S’
This is predominantly used to link various transactions and blocks. So each transaction in the block defines a valid state transition using the above functions from one transaction to another. The state, however, is not stored anywhere in the block and is calculated correctly only by starting from the genesis state of that particular block, for every transaction in that block. This finally gives an output of S[n] which will act as S[0] for the next block.
The order of the transactions is of prime importance because if B creates a transaction involving funds (UTXO) that have been sent (created) by A, then the transaction done by A must come before B for the block to be valid.
The condition of proof of work required is that the double-SHA256 hash of every block which is a 256-bit number must be less than a dynamically adjusted target. These dynamic targets vary from time to time so that the miners provide ample computational power to confirm their proof of work. Also, since the SHA256 function is completely pseudo random and unpredictable, the only way to crack it is by simple trial and error or brute force.
Suppose the dynamic target is set at ~2150 , then the network must achieve an average of 2(256–150) which equals 2106 tries before a valid block is found. This dynamic target is reset every 2016 blocks and calibrated to new target value. A new block on an average is produced every ten minutes on the Bitcoin network. For all the heavy lifting that miners do by facilitating our transactions and solving complex math problems, they are given Bitcoins as reward. The initial reward was 25 BTC per block mined. Currently, the reward is 12.5 BTC per mined block. This is how bitcoins come into circulation. The Bitcoins awarded to miners are new bitcoins that are being unlocked from the 21,000,000 Bitcoins which is the hard limit of Bitcoins that can ever be in circulation.
WHAT HAPPENS IN THE EVENT OF AN ATTACK?
Now let us analyse the benefits of mining and how it prevents attacks. The following lines have been picked from the Ethereum white paper as the text is pretty much self-explanatory.
“The attacker’s strategy is simple:
Send 100 BTC to a merchant in exchange for some product (preferably a rapid-delivery digital good)
Wait for the delivery of the product
Produce another transaction sending the same 100 BTC to himself
Try to convince the network that his transaction to himself was the one that came first.
Once step (1) has taken place, after a few minutes some miner will include the transaction in a block, say block number 270. After about one hour, five more blocks will have been added to the chain after that block, with each of those blocks indirectly pointing to the transaction and thus “confirming” it. At this point, the merchant will accept the payment as finalized and deliver the product; since we are assuming this is a digital good, delivery is instant. Now, the attacker creates another transaction sending the 100 BTC to himself. If the attacker simply releases it into the wild, the transaction will not be processed; miners will attempt to run APPLY(S,TX) and notice that TX consumes a UTXO which is no longer in the state. So instead, the attacker creates a “fork” of the blockchain, starting by mining another version of block 270 pointing to the same block 269 as a parent but with the new transaction in place of the old one. Because the block data is different, this requires redoing the proof of work. Furthermore, the attacker’s new version of block 270 has a different hash, so the original blocks 271 to 275 do not “point” to it; thus, the original chain and the attacker’s new chain are completely separate. The rule is that in a fork the longest blockchain is taken to be the truth, and so legitimate miners will work on the 275 chain while the attacker alone is working on the 270 chain. In order for the attacker to make his blockchain the longest, he would need to have more computational power than the rest of the network combined in order to catch up (hence, “51% attack”).”
The above text shows how to gain control over the blockchain, the attacker has to have more processing power than 51% of the total blockchain which is probabilistically impossible for top coins.
Merkle Trees
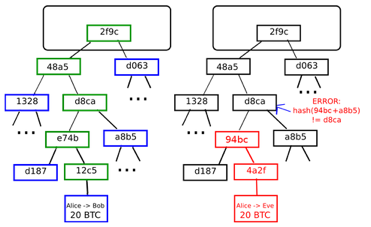
Merkle trees help maintain the uniqueness of a block. Merkle trees are a binary tree where each node has two children, and this goes all the way to the bottom to have individual leaf nodes which consists of transaction data. These leaf nodes build up to the top as shown in the below figure and end up in one ‘hash’. This hash of a block consists of a timestamp, nonce, previous block hash and the root hash of the Merkle tree as shown in the image on the left.
Now, the beauty of cryptographic functions is, even if one bit of input is changed, the whole encryption pattern changes and the intermediate hash value output is different. This changes the hash value output of the overall block and is rejected by the blockchain because it does not have a valid proof of work. The output of a Merkle tree is a single hash which is secure enough to act as an assurance to nodes.
These nodes compare this hash from one source with another small part of the Merkle tree from another source to ultimately validate the authenticity of the block. A similar scenario is shown in the right side of the above image when a node rejects a block because its hash does not match with the data in Merkle tree.
As the data stored in the blockchain of bitcoin is continuously increasing, there will be a point at which average desktop computers would not be able to store all the data. This is where a protocol known as “simplified payment verification” (SPV) comes into play. This protocol lets nodes verify the proof of work using the hash in individual blocks. Such nodes are also called as ‘light nodes’. These light nodes download the block headers, verify the proof of work on the block headers, and then download only the “branches” associated with transactions that are relevant to them. Light nodes thus assure that the transactions are legit despite downloading only a very small portion of the blockchain.
Alternative Blockchain Applications
NameCoin
NameCoin lets you register names on a decentralized database.
Colored coins
Colored coins serve as a protocol to allow people to create their own digital currencies on the Bitcoin Blockchain.
Metacoins
Metacoin protocol is stored on top of Bitcoin but uses a different state transition function from Bitcoin. They provide a mechanism to create an arbitrary cryptocurrency protocol.
There are two ways to build a blockchain system. The first is building an independent network and the second includes building a protocol on top of Bitcoin. The first approach is difficult to implement because of the costs involved. Also, the number of applications that would run on the Blockchain do not demand a full-fledged independent network. The requirements of these applications are relatively less computer intensive.
The Bitcoin-based approach has the flaw that it does not inherit the simplified payment verification features of Bitcoin. SPV works for Bitcoin because it can use blockchain depth as a proxy for validity; at some point, once the ancestors of a transaction go far enough back, it is safe to say that they were legitimately part of the state. A fully secure SPV meta-protocol implementation would need to backward scan all the way to the beginning of the Bitcoin Blockchain to determine whether or not certain transactions are valid.
Scripting
Bitcoin protocol does handle a primitive version of a concept known as ‘smart contracts’. UTXO in Bitcoin can be owned not just by a public key, but also by a complicated script expressed in a simple programming language. In this scenario, after a transaction, UTXO must provide data that satisfies the script. Afterall, even the basic public key ownership mechanism is implemented via a script which is verified using elliptic curve signatures. The script returns 1 if the verification is successful and returns 0 otherwise.
This can be further controlled to write a script that requires signatures from two out of a given three private keys to validate (“multisig”). This is a use case for large conglomerate corporate accounts, secure accounts and escrow situations. These smart contract scripts can be modified to do numerous actions depending on the use case.
However, there are several limitations in the Bitcoin scripting language:
Lack of Turing Completeness — Loops are not available to prevent infinite loop situations but to write a smart contract in a language that is not Turing complete can be considerably daunting.
Value Blindness — The UTXO script is not able to determine if the value of BTC has changed when compared to USD.
Lack of State — A UTXO can either be spent or unspent. To create complicated smart contracts that might include two stage cryptographic verification on the Bitcoin network is not possible.
Blockchain Blindness — UTXO also does not have access to nonce, timestamp or previous block hash. This limits the application of Bitcoin in many fields.
“Ethereum proposes to build an alternative framework that provides even larger gains in ease of development as well as even stronger light client properties, while at the same time allowing applications to share an economic environment and blockchain security.”
This concludes the interpretation of Part 1 of the Ethereum white paper. To summarise, this post gave us a general overview of how Bitcoin, the very first Cryptocurrency, functions. We will now move on to analyse how Ethereum is different from the Bitcoin protocol.