Programming Mythbusters! - Can You Unshuffle a Deck of Cards?

Image from Wikipedia
Ever hear someone say "If you shuffle it more than seven times, you're just putting it back in order"? I don't know how true that is, but I began to wonder if there was some point at all where the cards would in fact go back in order.
The Challenge
With 52 cards, is this possible? I will attempt tonight to write a program that does all this math for us to solve this problem. And I will be writing in C#.
Immediately, the first problems for success that come to mind are:
- shuffles are not always perfect
- initial cuts are not always perfect
- which side of the split deck will drop first?
The Testing
Simple Test
Well in a perfect shuffle where the bottom half of the deck drops first, we get this:
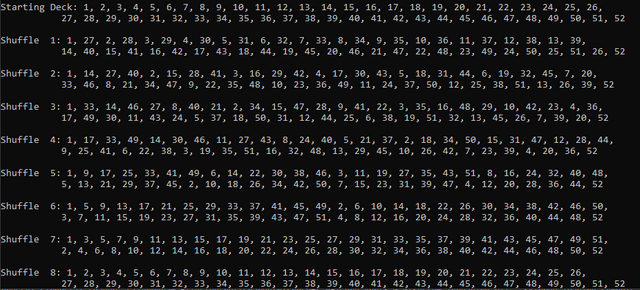
Um...
The deck is back in order.
Well, I guess myth kinda confirmed...
Start with the other hand
Let's swap it around next and see how many times it'll take when the first half of the cut drops first...

It comes together near the 26th shuffle. On the 26th, it's in backwards order. It should take another 26 to get back in forwards order.

Yep.
Adding complexity
But lets be realistic here. Us normal people can't shuffle perfect every time, and the first card that comes down may come from the former top half some times or the former bottom half. So let's add some complexity to this and see if we can bust-ish this myth with a more realistic view. Points to consider:
- first card down won't necessarily always come from the same hand
- some number of cards will come down each time, not always just one
Ok let's start with the alternating first card. That'll be easy.
Here I just added in a random variable random and used it to determine which side dropped the first card. I had to use 0,2 instead of 0,1 because in C# the random starts at the first number and ends just before the second. Effectively picking a random number between 0 and 1.99 and then chopping off the decimal. Following that is my shuffling code.
Random random = new Random();
...
int[] newDeck = Shuffle(firstHalf, secondHalf, random.Next(0,2));
...
private static int[] Shuffle(int[] a, int[] b, int first)
{
int[] newShuffle = { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 };
if (first == 0)
{
for (int x = 0; x < newShuffle.Length; x += 2)
{
newShuffle[x] = a[(int) x / 2];
newShuffle[x + 1] = b[(int) x / 2];
}
}
else
{
for (int x = 0; x < newShuffle.Length; x += 2)
{
newShuffle[x] = b[(int) x / 2];
newShuffle[x + 1] = a[(int) x / 2];
}
}
return newShuffle;
}
In these results, 52 shuffles didn't do anything spectacular. On the 27th shuffle, the 1 card and the 52 card were back in place. But then I started noticing a peculiar pattern. If you add up the first number and the last number of any shuffle, it comes out to 53 (1 plus 52 for example). Same with card 2 and card 51. Same with card 26 and card 27. each opposing pair adds up to 53. While the card positions are different throughout the shuffles, the pairs always stick together at opposite ends of the deck! It's crazy. on shuffle 8, the first card is 30 and the last card is 23. On shuffle 40, the numbers 30 and 23 are in positions 21 and 32, both 5 cards from the middle pair. (by the way, their positions will also add up to 53.)
But let's see if we can't find out how many shuffles it will take to get back in order (I'll include backwards order too). To make the output less cumbersome, I only wrote to console if the first 2 cards AND the last two cards were in order.
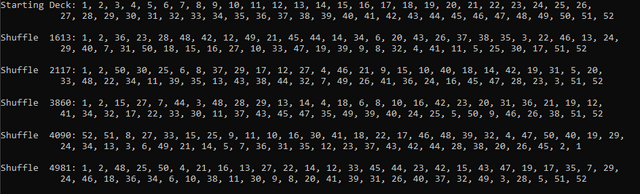
As you can see, I got nowhere close in the first 5000 shuffles.
Maybe in 50,000?
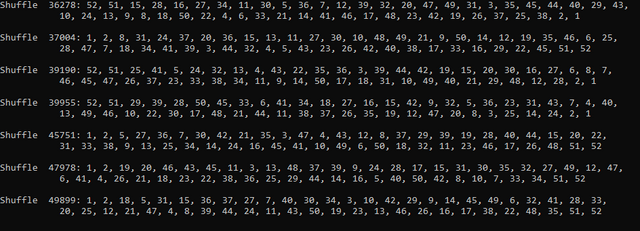
No closer. Not even in 50,000 shuffles did the third card ever get in place.
Ok, but one final thing to do. Like I said earlier, we're not gonna shuffle a deck this perfectly every time. More than one card may drop. I might have to rewrite my shuffler to make this happen.
To change the cut, I added another randomrand.Next(-3,4);to modify the location where the split happens. Then I had to put my shuffler into a while loop and drop one card at a time from the bottom up just like you were shuffling it by hand.
private static int[] Shuffle(int[] deck, int first)
{
int[] newShuffle = { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 };
int[] a;
int[] b;
Random rand = new Random();
Split(deck, (deck.Length / 2 + rand.Next(-3, 4)), out a, out b);
int cardsInA = a.Length;
int cardsInB = b.Length;
int cardsUsed = 0;
int drop = 0;
while (cardsInA>0 || cardsInB>0)
{
if (first == 0)
{
drop = GetCardsDropped();
for (int x = 0; x < drop; x++)
{
if (cardsInA > 0)
{
newShuffle[51 - cardsUsed] = a[cardsInA - 1];
cardsInA--;
cardsUsed++;
}
}
drop = GetCardsDropped();
for (int x = 0; x < drop; x++)
{
if (cardsInB > 0)
{
newShuffle[51 - cardsUsed] = b[cardsInB - 1];
cardsInB--;
cardsUsed++;
}
}
}
else
{
drop = GetCardsDropped();
for (int x = 0; x < drop; x++)
{
if (cardsInB > 0)
{
newShuffle[51 - cardsUsed] = b[cardsInB - 1];
cardsInB--;
cardsUsed++;
}
}
drop = GetCardsDropped();
for (int x = 0; x < drop; x++)
{
if (cardsInA > 0)
{
newShuffle[51 - cardsUsed] = a[cardsInA - 1];
cardsInA--;
cardsUsed++;
}
}
}
}
return newShuffle;
}
To randomize the number of cards that dropped, I tried to make it feel a little more natural where 1 was most likely, 2 a little less, and so on up to 5 cards.
private static int GetCardsDropped()
{
Random rand = new Random();
int f = rand.Next(0, 3);
if (f == 1)
return rand.Next(1, 4);
else if (f == 2)
return rand.Next(1, 6);
else
return 1;
}
And after 9 shuffles, we have a much nicer random assortment of cards.
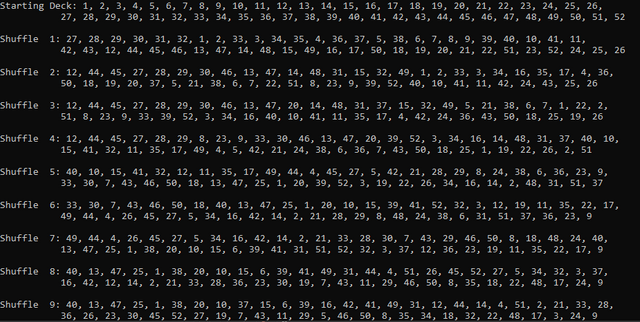
Now let's see how many in 50,000 shuffles come close to being in order. I'll be more lenient and just check the first 3 cards.
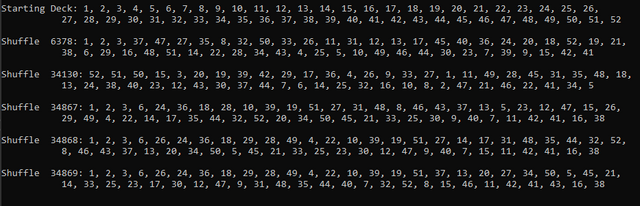
This is the best I've gotten so far. Some shuffles turned up one or two, some turned up nothing.
Wait, I may not be being fair. The first few cards may be off, but that doesn't mean parts aren't in order. How about we check for trends to see if we may have a series of numbers in order somewhere other than the beginning. I wrote another function to check for these trends:
private static bool cardTrend(int[] newDeck, int v)
{
int direction = 0; // 0 = start. 1 = up. 2 = down.
int trend = 0; // how many in a row are up or down
for (int x = 0;x<newDeck.Length-1;x++)
{
if (newDeck[x + 1] == newDeck[x] + 1)
{
if (direction == 0 || direction == 1)
{
direction = 1;
trend++;
}
else
{
direction = 2;
trend = 1;
}
}
else if (newDeck[x + 1] == newDeck[x] - 1)
{
if (direction == 0 || direction == 2)
{
direction = 2;
trend++;
}
else
{
direction = 1;
trend = 1;
}
}
else
{
direction = 0;
trend = 0;
}
}
if (trend >= v)
return true;
else
return false;
}
And then I call it with this.
if (cardTrend(newDeck, 4))
{
Console.WriteLine("Shuffle " + (x + 1) + ": " + WriteDeck(newDeck));
Console.WriteLine("");
}
And in several rounds of 50,000 shuffles, I have net been able to find a trend 5 cards long. Not even 4 cards long.
The Conclusion
Unless you're a card shuffler robot or professional, you probably will never successfully "unshuffle" your deck. But with enough practice, you could get good enough in your shuffle to only let one card down at a time. If you can do that regularly, then you will be able to unshuffle your deck.
Because of the amount of practice involved, I'm gonna give this myth...
PLAUSIBLE
Thanks you for reading. If you enjoyed this coding adventure and would like me to do more, give me an upvote and maybe even a comment with a suggestion for another programming mythbusters episode.