机器学习:数据预处理之归一化
归一化的目的:
1、归一化后加快了梯度下降求最优解的速度
2、归一化有可能提高精度
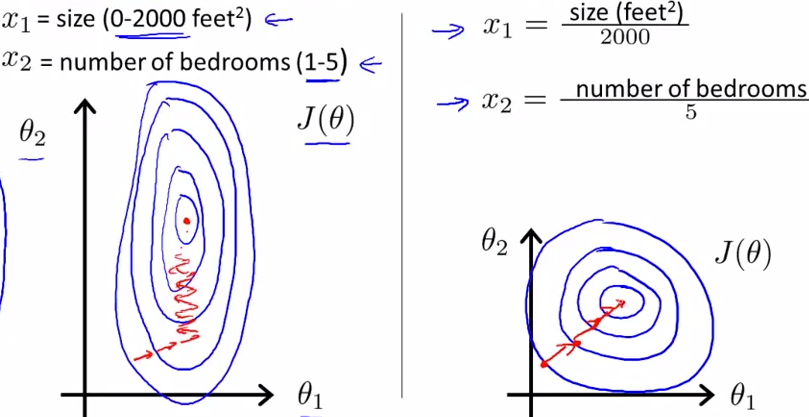
如下图所示,蓝色的圈圈图代表的是两个特征的等高线。其中左图两个特征X1和X2的区间相差非常大,X1区间是[0,2000],X2区间是[1,5],其所形成的等高线非常尖。当使用梯度下降法寻求最优解时,很有可能走“之字型”路线(垂直等高线走),从而导致需要迭代很多次才能收敛;
而右图对两个原始特征进行了归一化,其对应的等高线显得很圆,在梯度下降进行求解时能较快的收敛。
因此如果机器学习模型使用梯度下降法求最优解时,归一化往往非常有必要,否则很难收敛甚至不能收敛。
计算样本距离时,如果特征向量取值范围相差很大,如果不进行归一化处理,则值范围更大的特征向量对距离的影响更大,实际情况是,取值范围更小的特征向量对距离影响更大,这样的话,精度就会收到影响
方法:
1、线性函数归一化(Min-Max scaling)
线性函数将原始数据线性化的方法转换到[0 1]的范围,归一化公式如下:
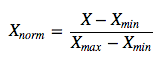
该方法实现对原始数据的等比例缩放,其中Xnorm为归一化后的数据,X为原始数据,Xmax、Xmin分别为原始数据集的最大值和最小值。
这种归一化方法比较适用在数值比较集中的情况。这种方法有个缺陷,如果max和min不稳定,很容易使得归一化结果不稳定,使得后续使用效果也不稳定。实际使用中可以用经验常量值来替代max和min。
2、0均值标准化(Z-score standardization)
0均值归一化方法将原始数据集归一化为均值为0、方差1的数据集,归一化公式如下:
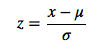
其中,μ、σ分别为原始数据集的均值和标准差。
标准差公式为:
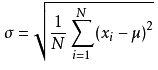
该种归一化方式要求原始数据的分布可以近似为正态分布,否则归一化的效果会变得很糟糕。
以上为两种比较普通但是常用的归一化技术,那这两种归一化的应用场景是怎么样的呢?什么时候第一种方法比较好、什么时候第二种方法比较好呢?下面做一个简要的分析概括:
1、在分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候,第二种方法(Z-score standardization)表现更好。
2、在不涉及距离度量、协方差计算、数据不符合正太分布的时候,可以使用第一种方法或其他归一化方法。比如图像处理中,将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。
3)非线性归一化
经常用在数据分化比较大的场景,有些数值很大,有些很小。通过一些数学函数,将原始值进行映射。该方法包括 log、指数,正切等。需要根据数据分布的情况,决定非线性函数的曲线,比如log(V, 2)还是log(V, 10)等。(未学习)
这个太复杂,真心看不懂!
…………………………………………………………………
烦请继续为我点赞,我会回赞的(✪▽✪)