SÍNTESIS DE REDES PARA FILTRADO DE SEÑALES

DEFINICION DE SINTESÌS DE REDES.

Me permito definir la síntesis de red como lo hace el libro de Alexander Sadiku, el cual afirma que la síntesis de red es el proceso para obtener una red apropiada a fin de representar una función de transferencia dada. La síntesis de red es más fácil aplicarla en el dominio de s que en el dominio del tiempo.

En el análisis de red, encontramos la función de transferencia de una red dada. En la síntesis de red invertimos el proceso, es decir; se requiere que encontremos una red conveniente que represente una función de transferencia dada. Debido a que la síntesis de red consiste en determinar una red tipo que represente una función de transferencia dada, podemos afirmar que existen muchas respuestas diferentes o (posiblemente ninguna) porque hay muchos circuitos que se usan para representar la misma función de transferencia, por el contrario en el análisis de red, hay solo una repuesta.

En el diseño de filtros analógicos se combinan tanto el análisis de redes como el método de síntesis de red, siendo la síntesis de red, el corazón del diseño de los filtros modernos por el método de las perdidas por inserción.

La síntesis de red constituye un curso entero por sí mismo y requiere alguna experiencia y destreza para encontrar la red más apropiada a los requerimientos del diseño, pero en este artículo solo se abarcará lo que se necesita para el diseño de nuestros filtros. La síntesis de red, puede ser activa o pasiva, dependiendo de la naturaleza de sus elementos.

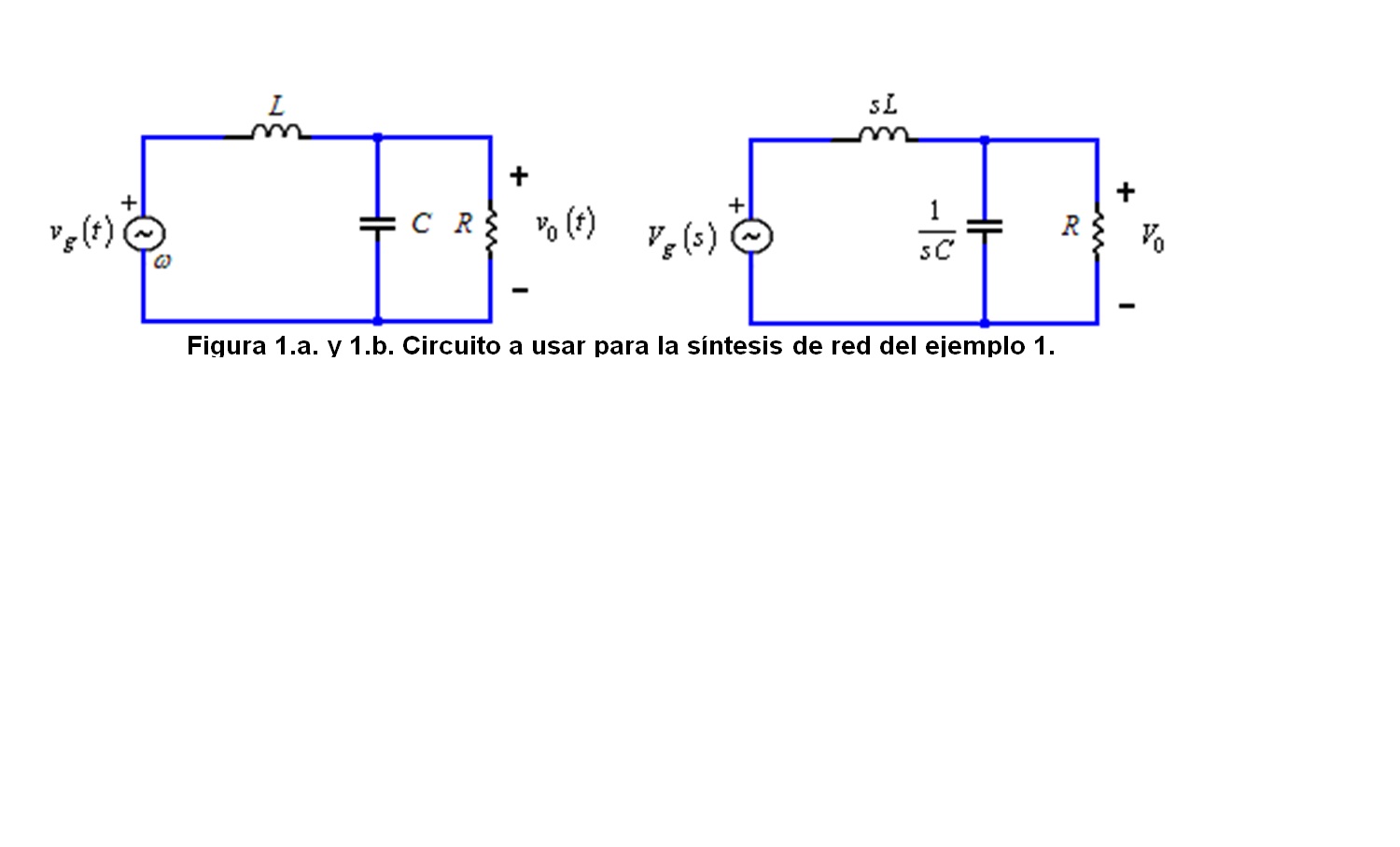
Ejemplo 1: Dada la siguiente función de transferencia H(s), sintetice dicha función, utilizando el circuito pasivo de la figura 1: a) seleccione para R=5 Ω; encuentre L y C b) seleccione para el caso de normalización R=1 Ω; encuentre L y C
H(s)=10/(s^2+32s+10) (Ec. 1)

()

Solución: El equivalente en el dominio de s para el circuito de la figura 1.a, se muestra en la figura 1.b. Sabemos por arreglo de redes que la combinación en paralelo de R y C da:
R║1/sC; Zeq1=R/(1+sRC)

Usando el principio de división de tensión, obtenemos la siguiente función de transferencia:
                    
                                                         (V0(s))/(Vi (s))=(1⁄LC)/(s^2+s/RC+1⁄LC)                        (Ec. 2)

Al comparar con la función de transferencia H(s) dada en (Ec.1), con la obtenida en la ecuación (Ec.2), resulta que:
1/(LC)=10; 1/(RC)=3

   a) Seleccionando R=5, entonces tenemos:
            
                                C=1/(3R)=66.67 mF      L=1/(10C)=1.5 H

b) Seleccionando R=1 Ω , entonces que:, entonces que
                
                                C=1/(3R)=0.333 F       L=1/(10C)=0.3 H

Ejemplo 2: Dada la siguiente función de transferencia H(s), sintetice dicha función, utilizando el circuito activo de la figura 2.

                                  H(s)= (10^6)/(s^2+100s+10^6 )             (Ec. 3)

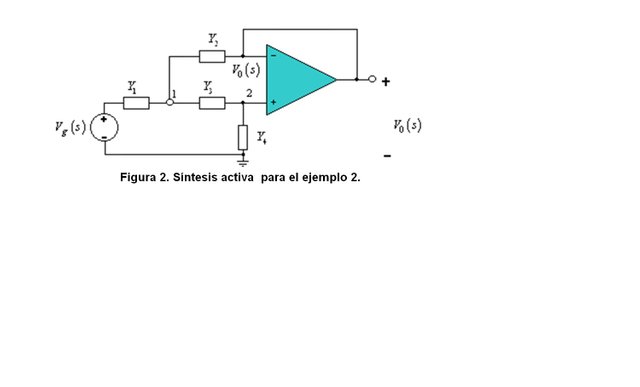
Aplicando análisis nodal en los nodos 1 y 2 y utilizando la teoría del cortocircuito virtual OPAMP, obtenemos, la siguiente función de transferencia:

                                 H(s) = (Y1Y3)/(Y1Y3+Y4(Y1+Y2+Y3))                    (Ec.4)

Para sintetizar la función de transferencia H(s), dada en la ecuación 3, la comparamos con la obtenida en la ecuación 4. Para esto hay que tomar en cuenta dos aspectos: 1). Y1Y3 no debe contener a s, porque el numerador de H(s) es constante. 2). La función de transferencia es de segundo orden, lo que implica que debemos tener dos capacitores. Debido a estos dos puntos, debemos hacer Y1Y3 resistivas y hacemos Y2Y4 capacitivas. Es decir que:

        Y1=1/R1   Y2=sC1    Y3=1/R2   Y4=sC2                (Ec.5)

Sustituyendo la ecuación 5 en la ecuación 4, desarrollando y agrupando los términos, nos queda entonces:

      H(s)=(1 ⁄((R1R2C1C2)))/(s^2+(s(R1+R2)) ⁄((R1R2C1))+1 ⁄((R1R2C1C2)))    (Ec.6)

Comparando (6), con la ecuación dada (3), notamos que:
(1 ⁄(R1R2C1C2))=10^6 ((R1+R2)) ⁄ ((R1R2C1))=100
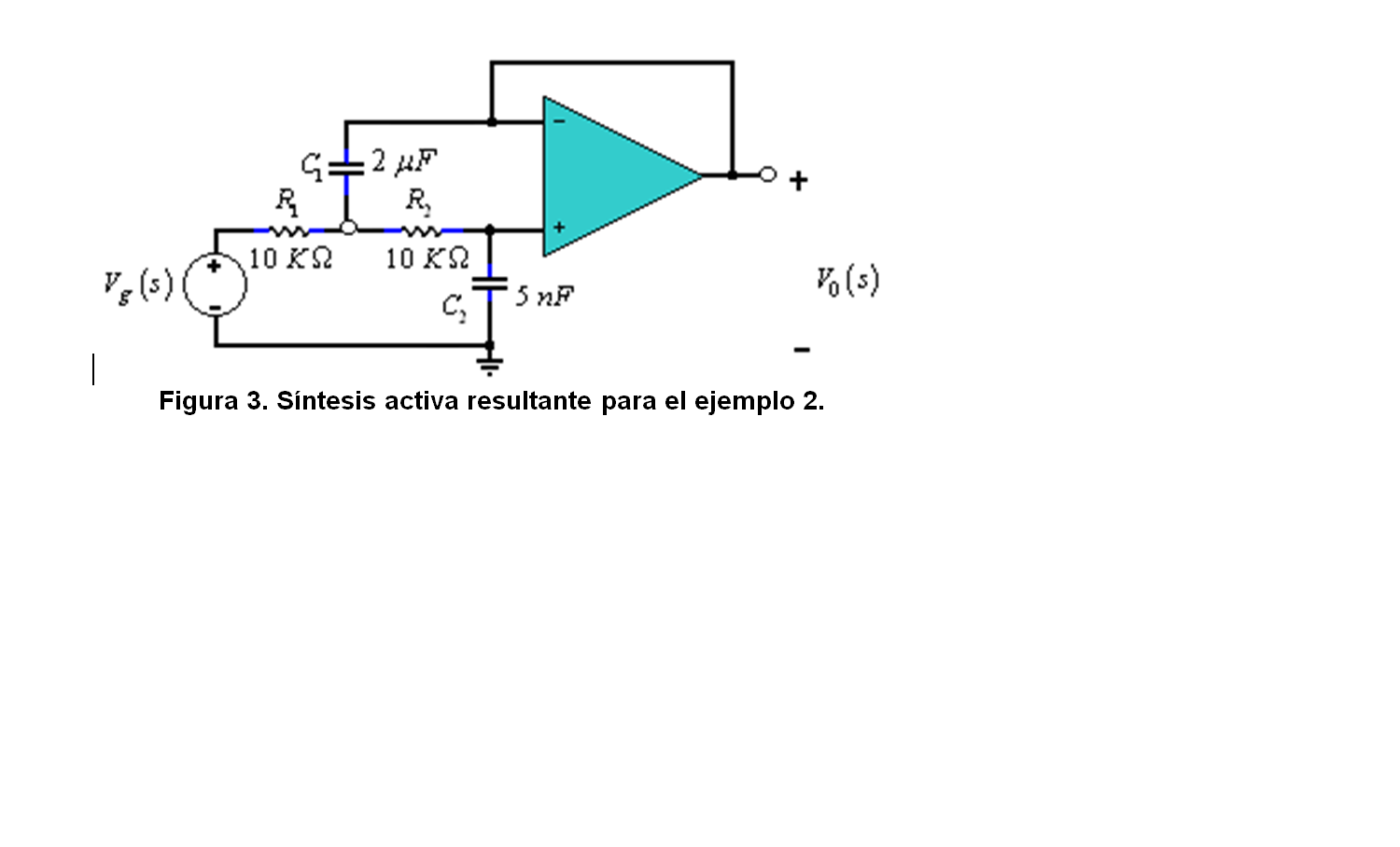
Si seleccionamos R1=R2=10kΩ, entones resulta:

    C1=((R1+R2) ⁄ (100R1R2))= 2μF         C2=(10^(-6)⁄(100R1R2C1)) = 5nF
De esta forma, la función de trasferencia dada se ha sintetizado en el circuito que se muestra en la figura 3.