"SLC-S22W2/Equations and inequalities."
I am @hudamalik20 from Pakistan. I hope you're all doing well and having a great time in life. Today, I am excited to participate in the learning contest "SLC-S22W2/Equations and Inequalities," organized by @khursheedanwar.
Through this contest, I am revisiting the algebra I studied in school, which will not only help me strengthen my understanding but also prepare me to teach others, including my siblings. So, let's get started.


Homework tasks
• Task 1
• Explain difference between linear and quadratic equations. Provide examples of each type of equation and describe their general forms.
When we study algebra, we come across many types of equations as I have studied in schoo so through this learning contest, I'm revising everything I learned in school.. Both involve variables like and , but their graphs and behavior are differennt..
Linear Equation
A linear equation is the simplest type of equation that forms a straight line when we plot it on a graph. Its general form looks like this:
So so gove you its type example..
y = mx + c
So in this:
m is the slope (to see how steep the line is).
And c is the y intercept (where the line crosses the y-axis).
So for this I give you example ..
y=2x+1 as I have solved this example on register .
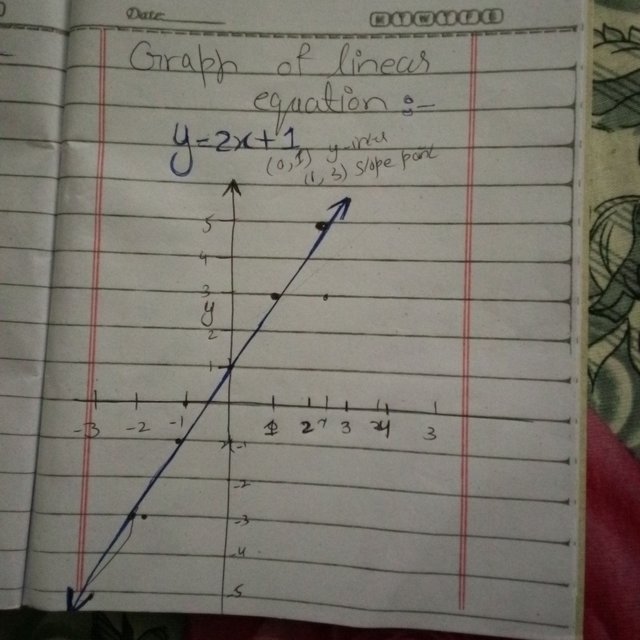
First, we calculate some points:
When 𝑥=0, then
y=2(0)+1=1 → Point is (0,1)
When 𝑥=1, then
y=2(1)+1=3 → Point is (1,3)
When 𝑥=−1 then
y=2(−1)+1=−1 → Point is (−1,−1).
They have ways a straight line.
The slope (m) tells us how fast y changes with x.
So the simple relationships like w measur speed, cost, or distance are often linear.
Quadratic Equation
A quadratic equation is a bit more complex. Its graph forms a U shaped curve, called a parabola.
So it's he general form is:
y = ax^2 + bx + c
So in this :
a,b,c are constants.
The parabola opens upwards if a> 0 and downwards if a<0.
So this is quadratic example as I have solved in the image :
y=x^2-3x+2
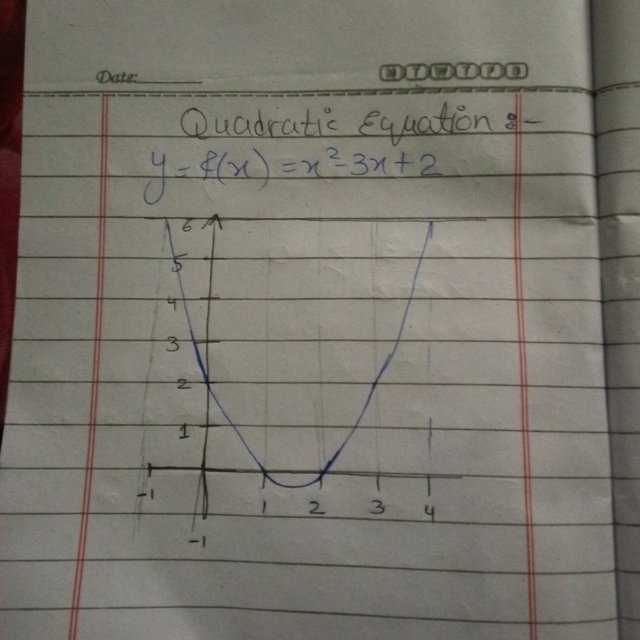
So first we calculate some points:
When 𝑥=0, then
y=(0)^2-3(0)+2=2 → Point is (0,2)
When 𝑥=1, then
y=(1)^2-3(1)+2=0 → Point is (1,0)
When 𝑥=2 then
y=(2)^2-3(2)+2=0 → Point is (2,0).
So then I draw a smooth U-shaped curve through them.
So the Quadratic equations are often used to represent things like projectile motion (e.g., how a ball flies through the air).
Key Differences
| Feature | Linear Equation | Quadratic Equation |
|---|---|---|
| Graph Shape | Straight Line | U-shaped Parabola |
| General Form | y = mx + c | y = ax² + bx + c |
| Highest Power of x | 1 | 2 |
| Example | y = 2x + 1 | y = x² - 3x + 2 |
• Task 2
• Describe two different types of inequalities(Which are not explained in course). Provide examples of each type of inequality and explain how to solve them.
There are two main types of inequalities, and one of them involves absolute value inequalities. Here's how I would explain it step by step, including examples and how to solve them:
1. Absolute Inequality
Absolute value inequalities deal with the distance of a number from zero on the number line. so in thus absolute value we ignores the sign of the number, so it can represent both positive and negative values.
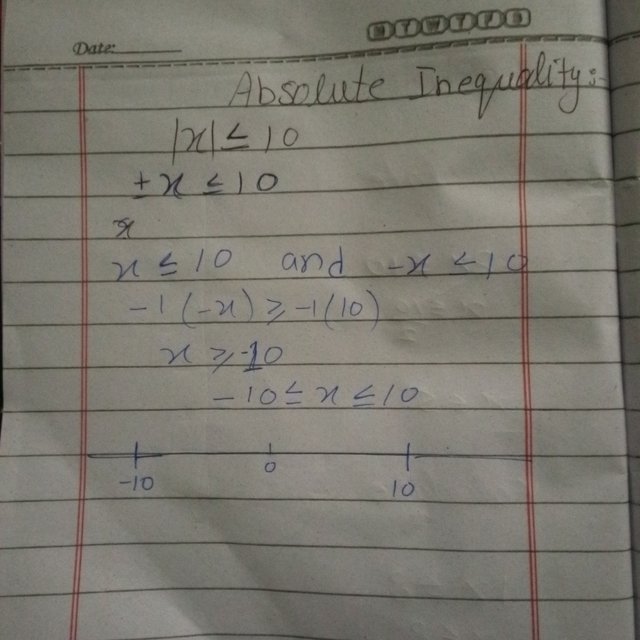
So the Example 1: |x| ≤ 10
This means the absolute value of is less than or equal to 10. To solve this:
So we break it into two inequalities:
-10 <=x <= 10
So this tells us x is any value between -10 and 10, they can be -3,5,8 etcc.
2.Rational Inequality
A rational inequality is a comparison that involves a fraction where the numerator and denominators.. ISo it tells us where the fraction is positive, negative, or zero. For example in this x-3/x+2>0 asks us to find the values of x where this fraction is greater than zero.
To solve it, the first step we have to understand is that the numerator and denominator determine the behavior of the fraction. The fraction equals zero when the numerator is zero and is undefined when the denominator is zero.
So In this case, by setting x-3=0 gives usbx=3 , and setting x+2=0 gives x=-2 . So by this we foind out tese values are the critical points that divide the number line into intervals.
Next, I divided the number line into three intervals as in mlthe image I have shared with you to determine whether the fraction is positive or negative in each interval,..

I chose a test value from each section and substituted it into the inequality. For x<-2 , I tested x=-3, and the fraction was positive. For , I tested , and the fraction was negative. For -2<x<3, I tested x=0, and the fraction was positive.
Based on these tests, I concluded in the answer that the fraction is positive for x<-2 and x>3 .
• Task 3
• Solve the following linear equation: 2x + 5 = 11.Show step-by-step solution and share its practical example of how this equation can be applied in real life scenario.
In this question, we had to solve a linear equation, which I solved on my notebook, and I shared the step-by-step solution. I hope my answer will be correct.
To simplify the equation, I moved the constant term from the left side to the right side. This was done by subtracting from both sides of the equation:
2x + 5 = 11
2x = 6
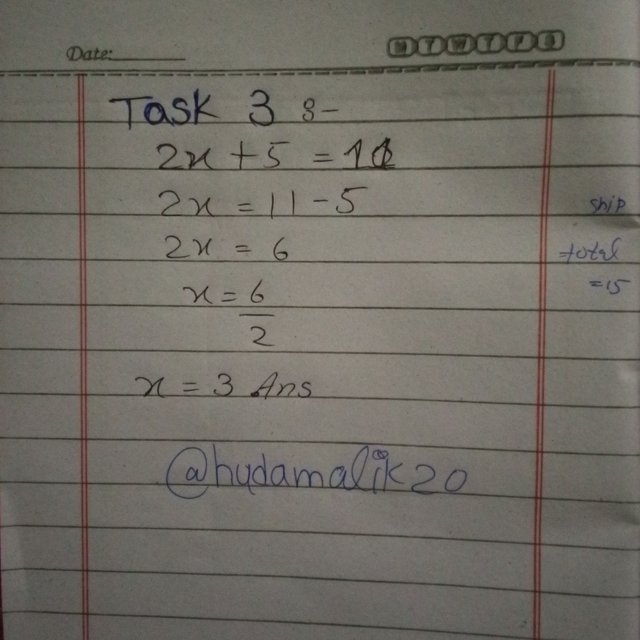
Practical example
So suppose this as I am shopping online, and I decide to buy 2 shirts on Amazon.. The shipping fee is $5, and the total amount I pay for the purchase is $11. I want to find out how much one shirt costs, including the shipping fee.
- The total cost is $11, which includes both the cost of the shirts and the shipping fee.
- The shipping fee is $5, so I subtract that from the total cost:
$11 - $5 = $6 (This is the total cost of the shirts).
- Since I bought 2 shirts, I divide the total cost of the shirts by 2:
$6 ÷ 2 = $3 per shirt.
• Task 4
Scenario: Tom's Bakery
How many cakes can Tom make?
So with the given ingredients Tom can make make one cake:
Flour: 2 cups
Sugar: 1 cup
Cocoa Powder: 0.5 cups
Tom has the following quantities of ingredients:
Flour: 10 cups
Sugar: 8 cups
Cocoa Powder: 4 cups
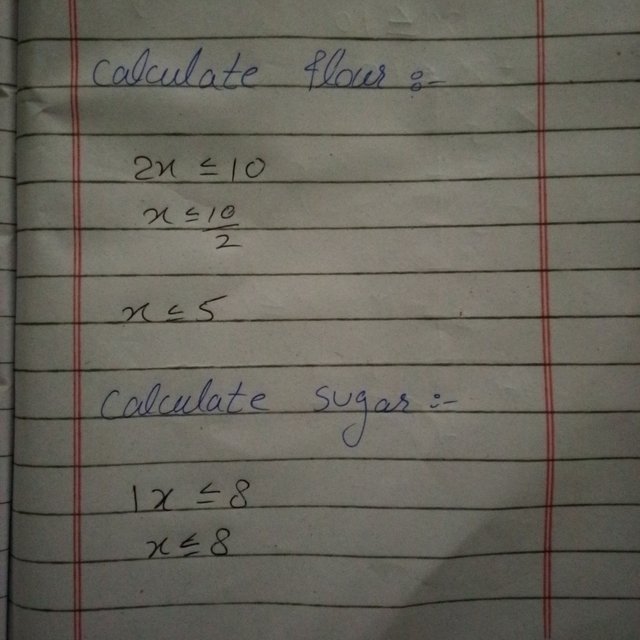
Calculate based on flour
To find how many cakes Tom can make using flour, I did this:
One cake needs 2 cups of flour, and Tom has 10 cups. I set up the equation:
2x ≤ 10
I calculated x by dividing 10 by 2:
x = 10 ÷ 2 = 5
So, based on flour, Tom can make 5 cakes.
Calculate based on sugar
Next, I checked for sugar. One cake needs 1 cup of sugar, and Tom has 8 cups. I set up this equation:
1x ≤ 8
I calculated x:
x = 8 ÷ 1 = 8
So this .means Tom can make 8 cakes using sugar.
Calculate based on cocoa powder
Then, I checked for cocoa powder. One cake requires 0.5 cups, and Tom has 4 cups. I set up this equation:
0.5x ≤ 4
I calculated x by dividing 4 by 0.5:
x = 4 ÷ 0.5 = 8
So, based on cocoa powder, Tom can make 8 cakes.
Then finally, I compared all the values. The limiting factor is flour, which only allows Tom to make 5 cakes.So, I concluded that Tom can make a maximum of 5 cakes.
Can Tom make 6 cakes based on sugar?
Here, I checked if Tom has enough sugar to make at least 6 cakes.
One cake requires 1 cup of sugar, and Tom has 8 cups. I set up the equation:
1x ≥ 6
To solve, I calculated:
x = 6 ÷ 1 = 6
Since Tom has 8 cups, which is more than 6, I concluded that yes, Tom can make 6 cakes based on sugar.
Ashley's trip fuel problem
Ashley needs to drive 240 miles, and her car has a fuel efficiency of 20 miles per gallon. She already has 2 gallons of fuel and wants to finish the trip with at least 1 gallon of fuel remaining.
Calculate total fuel required
I calculated the total fuel needed by dividing the distance by the fuel efficiency:
240 ÷ 20 = 12 gallons
How much fuel needed
Next, I calculated how much more fuel Ashley needs. She already has 2 gallons but wants to finish the trip with 1 gallon remaining.

I set up the inequality:
x + 2 ≥ 12 - 1
I simplified it like this:
x + 2 ≥ 11
x ≥ 11 - 2
x ≥ 9
So, I concluded that Ashley needs to buy at least 9 gallons of fuel to complete her trip and have 1 gallon left over.
That's it from today's blog I hope you will like it. With best wishes ❤️. Now I like to invite @tammann, @josepha and @norat to participate in this amazing contest.
Thanks alot for reading ❤️🤗 .
My introduction post
