The Brakey Method for Transparency & Alternative Voting Methods for Proportional Representation

As our goal is to provide for honest elections of representatives, of the people, for the people, and by the people, we need to roll up our sleeves and dive into the possibilities. A large number of various voting systems are in practice around the world and put into use for various types of elections by regions and country, between governments and corporations, and adopted to suit the occasion. Our current system, first past the post, is a winner take all system which results in a large number of disenfranchised voters. The number of votes not cast in many elections would be sufficient to change the outcome if voters had confidence that their vote counted and that the representatives on their ballots would sufficiently represent them enough to motivate them to vote.

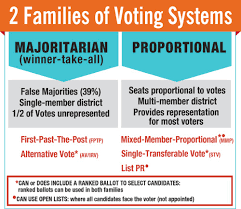
Studying voting methods it is often difficult to differentiate the fine details of each due to the similarity of concepts such as the difference between Majority Voting (more of the votes) vs. Plurality Voting (the most votes), but with each method, the winner is different, even though the votes have remained the same.

We need to examine the available voting methods and develop new methods for the future incorporating the technology we have available to increase transparency and provide for independent confirmation of reporting for accountability. Each state has the authority to regulate it's own elections and choose the method for the collection of the votes and the mechanisms for reporting the votes to it's constituents. Work on getting The Brakey Method going in your location. It is, at this time, the most important thing you can to do protect the counting of the vote. Brakey Method = transparency & auditability of the vote.

Votes counted from digital ballot images (BIs) as paper ballots are scanned and many states are destroying the paper ballots and the ballot images. Demand ballot images be preserved & released to public for a verified count! This authority has been called into question in recent years with many individuals uncomfortable with the lack of transparency and the ability to manipulate the totals without oversight or independent verification free from a conflict of interest if manipulation of the votes were to occur. Using The Brakey Method, the public would be able to independently verify the reporting of the count of the ballots cast in any given election, without compromising the sanctity of the voting process. Regardless of the voting method employed, instituting the Brakey Method would increase the public trust in the voting process, but would not change the voting system or process.

The majority criterion is a single-winner system which states that "if one candidate is preferred by a majority (more than 50%) of voters, then that candidate must win". Some methods that comply with this criterion include any Condorcet method, instant-runoff voting, Bucklin voting, and plurality voting. The majority criterion was originally defined in relation to methods which rely only on voted preference orders of the candidates. Thus, its application to methods which give weight to preference strength is in some cases disputed.

Some such methods, such as the Borda count and range voting, fail the criterion under any definition. For others, such as approval voting and majority judgment, the system may pass or fail depending on the definition of the criterion which is used. Advocates of other voting systems contend that the majority criterion is actually a flaw of a voting system, and not a feature, since it can lead to a tyranny of the majority where a polarizing candidate is elected who is loved by a little over half of the population and hated by everyone else. Other systems are better at electing consensus candidates who have broader appeal, making them better representative of the population as a whole.

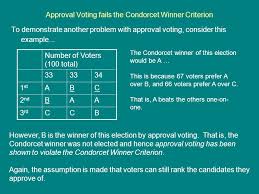
The Condorcet candidate (a.k.a. Condorcet winner) is the person who would win a two-candidate election against each of the other candidates in a plurality vote. For a set of candidates, the Condorcet winner is always the same regardless of the voting system in question. A voting system satisfies the Condorcet criterion if it always chooses the Condorcet winner when one exists. Any voting method conforming to the Condorcet criterion is known as a Condorcet method.

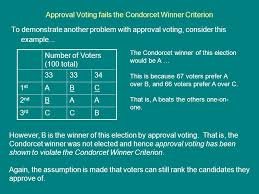
A Condorcet winner will not always exist in a given set of votes, which is known as Condorcet's voting paradox. When voters identify candidates on a 1-dimensional left to right axis and always prefer candidates closer to themselves, a Condorcet winner always exists. Real political positions are multi-dimensional, however, which can lead to circular societal preferences with no Condorcet winner.

The twentieth century economist Kenneth Arrow postulated the impossibility of a fair democratic election in his doctoral thesis, "A Difficulty in the Concept of Social Welfare" and has said "Most systems are not going to work badly all of the time. All I proved is that all (of them) can work badly at times." Known as Arrow's Impossibilty Theorem, the theorem states that no rank-order electoral system can be designed that always satisfies these three "fairness" criteria:

1. If every voter prefers alternative X over alternative Y, then the group prefers X over Y.
2. If every voter's preference between X and Y remains unchanged, then the group's preference between X and Y will also remain unchanged (even if voters' preferences between other pairs like X and Z, Y and Z, or Z and W change).
3. There is no "dictator" as no single voter possesses the power to always determine the group's preference.

Another notable theorem to familiarize yourself with when studying voting methods is May's Theorem which states that simple majority voting is the only anonymous, neutral, and positively responsive social choice function between two alternatives. Further, this procedure is resolute when there are an odd number of voters and ties (indecision) are not allowed.

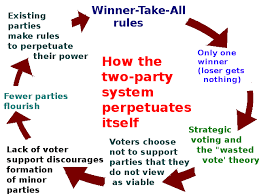
What's wrong with our voting system? It may be easier to start of with what is right if the goal was to complete the effort as quickly as possible. I hope that this information educates and inspires you to learn more about the possibilities in regards to voting methods. Regardless of the method which is chosen to choose a winner, the most important aspect of democratic elections is the sanctity of the vote and transparency in the counting of the votes to provide for free and honest elections. Support paper ballots and the Brakey method regardless of your preference of counting the votes and you will rest assured that your vote counts.

Work on getting The Brakey Method going in your location. Learn More about The Brakey Method: http://blackboxvoting.org/the-brakey-method/

Demand BIs be preserved & released to public for verified count! Get Involved at http://www.auditelectionsusa.org

& Learn More about the Types of Voting Systems

Plurality Voting: https://en.wikipedia.org/wiki/Plurality_voting

Plurality at Large Voting: https://en.wikipedia.org/wiki/Plurality-at-large_voting

First Past the Post: https://en.wikipedia.org/wiki/First-past-the-post_voting

Instant Runoff Voting: https://en.wikipedia.org/wiki/Instant-runoff_voting

The Borda Method: https://en.wikipedia.org/wiki/Borda_count

Coomb's Rule Method: https://en.wikipedia.org/wiki/Coombs%27_method

Approval Voting: https://en.wikipedia.org/wiki/Approval_voting

The Hare Method: https://en.wikipedia.org/wiki/Hare_quota

The Condorcet Method: https://en.wikipedia.org/wiki/Condorcet_method

Successive Reversal Method: https://en.wikipedia.org/wiki/Minimax_Condorcet
The Beatpath Method: https://en.wikipedia.org/wiki/Schulze_method

There are a number of videos available to become more familiar with the various voting methods including "Do Third Parties Destroy Democracy" Video Series by Carneades
with playlist available at youtube.com/user/carneadesofcyrene/playlists and the "History, Method, & Theory of Voting" at youtube.com/watch?v=FdWMMQINIt4

Learn more about Arrow's Impossibilty Theorem and May's Theorem on Wikipedia at wikipedia.org/wiki/Arrows_impossibility_theorem and wikipedia.org/wiki/Mays_theorem

Study the Majority Criterion and The Condorcet Criterion at https://en.wikipedia.org/wiki/Majority_criterion and https://en.wikipedia.org/wiki/Condorcet_criterion