"SLC-S22W6//Graphing and conic sections."

Steemian Friends,
Today, I will submit the homework for the @khursheedanwar Brother lesson in Week 06 of Steemit Learning Challenge 22. The lesson name is SLC S22W6//Graphing and Conic sections. I have loved Mathematics since childhood. It is my favourite subject. I hope everyone likes my homework.

Design By Canva

---

Task-01

---

---

Quadratic function:
A quadratic function is a polynomial function whose degree is 2. General form of quadratic function is f(x)= ax^2+bx+c,
Where a,b, & c are real numbers, and a is not equal to 0.

Example:
f(x)=3x^2+5x+3 is a quadratic function.

Where,
a=3
b=5
c=3
The degree is 2.

Exponential function:
We use the Exponential function to calculate population growth or decline, compound value and interest rate.
The general form of the exponential function is f(x)=ab^x
where, a= Initial Value
b= base
x=Exponent.

Here,
a is not equal to zero, and
b is not equal to 1
b>0.

Example:
f(x)=50(5.6)^x is an exponential function.

---

Differences:

---

Aspect	Quadratic Function	Exponential Function
General Form	f(x)= ax^2+bx+c	f(x)=ab^x
Example	f(x)=3x^2+5x+3	f(x)=50(5.6)^x
Symmetric	Quadratic Function is symmetric about vertex	Exponential Function no symmetry
Graph	Quadratic Function is parabola	Exponential Function is curved

---

Task-02

---

---

Here, I give two real-world examples of exponential and quadratic functions:

---

Exponential function:

Population Growth:
If the population of a country doubles every 10 years, the number of people P(t) over time (t) can be calculated as:

Radioactive decay:
We know that the amount of radioactive material decreases with time. For example, the mass M(t) after time t can be expressed as:

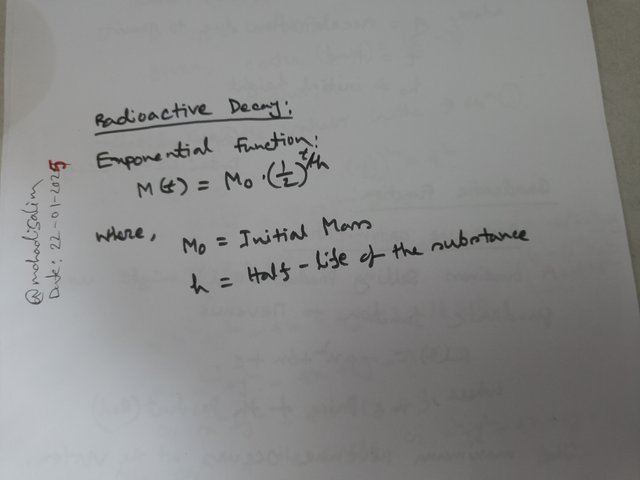
Projectile Motion:
If I throw a ball upwards, the quadratic function against the force of gravity will be as follows. Here, the initial height acts as a gravitational force over time.

Revenue Optimization:
I can write the price increase of a company's product rod as a quadratic function. Here, x is the price of the product. In the picture, I have shown it as a function.

Task-03

---

---

First, we know the equation of the circle, write (x-h)^2+(y-k)^2=r^2.

Then, the centre of the circle (h,k)=(2,-3) and radius r=4 in the above equation of a circle.

Then, by algebra, I get an equation, which is the equation of the circle. x^2+y^2-4x+6y=3.

---

---

I will solve the given equation using a quadratic formula.
The quadratic formula, x=-b+/-√b2-4ac/2a

Here,
a=2
b=5
c=-3
Substitute the values ​​in the above equation.

Then, doing algebra, I get two values ​​of x,
x=1/2 and -3.

Task-04

---

Scenario number 1

---

Suppose there's a satellite dish which is shaped like paraboloid.If equation of the paraboloid is given by y = 0.1x^2 then here x and y are measured in meters so now;

---

---

The graphical equation is,
y= 0.1x^2 and is a parabola.
Vertex at the origin (0,0).
I have shown the graph below.

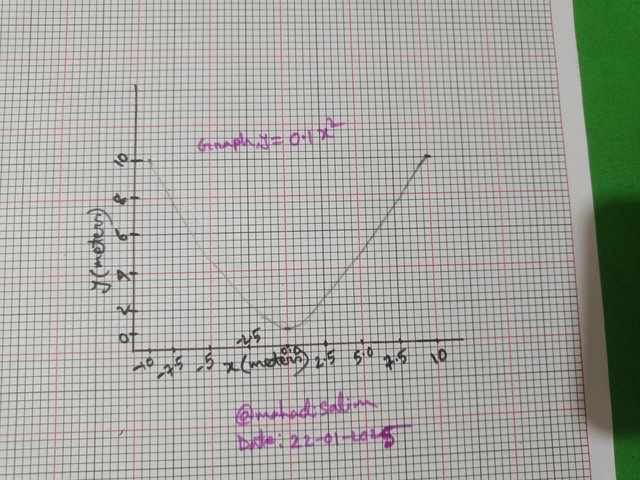
y=0.1x^2 is the parabola graph.
The parabola is a symmetric y-axis and opens upwards.

---

---

We know,
Parabola general form is, y=1/4f x^2.
Given the equation, y=0.1x^2.
I put the value of y into the parabola equation and get the focal length,
f= 2.5 meters.

---

---

The directrix for the parabola opening upwards is the horizontal line,
y= -f,
where,
f= focal length.

---

Scenario number 2

---

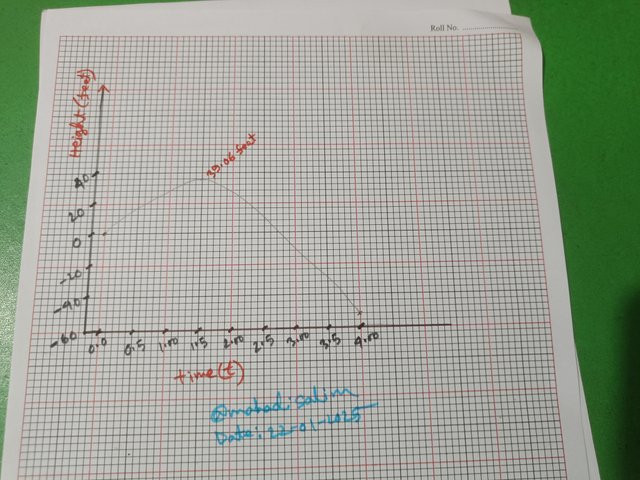
You need for suppose that there's a ball which is thrown in upward direction from ground with an initial velocity of 50 ft/s.Suppose if height of ball above ground is given by the equation h(t) = -16t^2 + 50t and here t is presenting time in seconds then;

---

---

I have graphed the equation h(t)=-16t^2+50t. Before plotting each graph, I had to solve for b and c. The graph shows that the ball took 1.56 seconds to reach 39.06 feet, and the ball hit the ground in 3.125 seconds.

---

---

We know,
The Parabola vertex equation formula is t= b/2a
where,
a= -16
b=50,
Put the value of a and b in the above equation, t= 1.5625.
Now, put the value of t into the equation,
h(t)= -16t^2+50t and do the algebraic calculation.
Then I get the height of the ball h(t)= 39.06 feet.Ans:

---

---

I get the equation in question by algebraic calculation,
h(t)=-16t^2+50t=0
to get two values ​​of t,
namely t=0 and t=3.125 s.
I have shown these values ​​through graphs.

---

SL No.	My Invited Steemit Friends
1	@memamun
2	@uzma4882
3	@lirvic