SLC S22W6//Graphing and Conic sections

_{Edited by Canva}

Hello steemians,

Here is my homework for SLC22 Week 6, with the corresponding tasks assigned by @khursheedanwar!

Task1:

Differentiate between quadratic and exponential functions with examples and general forms of each!

A quadratic function is written in the form f(x) = ax^2 + bx + c, where a, b and c are constants, and x is squared, the main characteristic of this function is that it produces a parabola in a graph, this parabola is symmetric, with a vertex which represents a maximum or a minimum, depending on whether a is negative or positive, for example, if f(x) = x^2 + 2x + 1 , its graph shows a symmetrical curve that opens upwards.

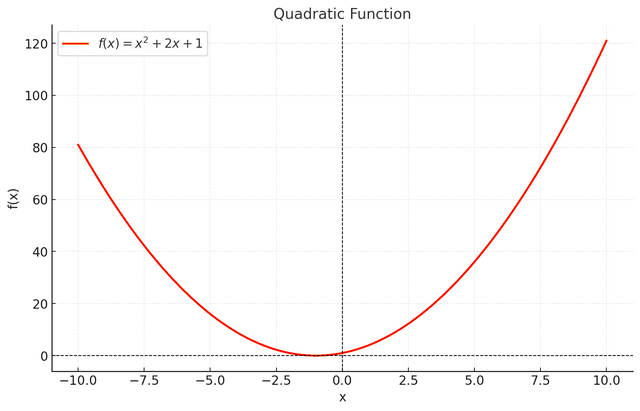
In contrast, an exponential function is written as f(x) = ab^x, where a represents the initial value and b, the base, is a positive number other than 1. In such a function, the variable x is in the exponent, resulting in rapid growth (if b > 1) or rapid decay (if 0 < b < 1), for example f(x) = 3 .2^x grows rapidly with x, showing an asymmetrical climb with a horizontal asymptote at y=0.

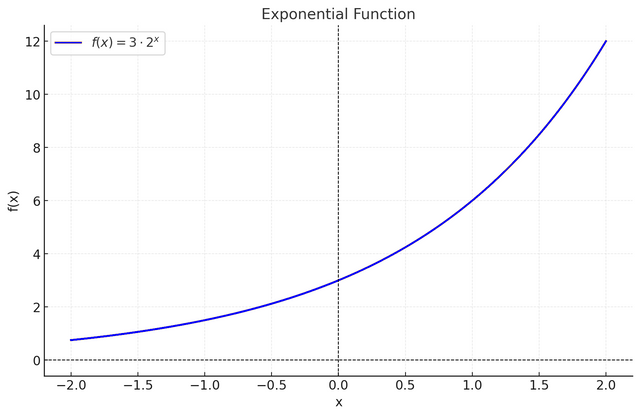
One of the big differences is in the behavior as x increases, for a quadratic function the growth is polynomial and relatively slow compared to an exponential function, where the growth or decay becomes very fast, moreover, applications vary: quadratic functions are often used to model trajectories or areas, while exponential functions are suitable for modeling growth or decay phenomena, such as compound interest or radioactive decay.

Appearance	Quadratic Function	Exponential Function
General Form	( f(x) = ax^2 + bx + c )	( f(x) = ab^x )
Key Feature	The (x^2) term dominates, creating a parabolic curve.	The (x) variable is in the exponent, causing rapid growth or decay.
Behavior	Slow to moderate growth depending on the value of (a).	Rapid growth or decay depending on the base (b).
Example	( f(x) = x^2 + 2x + 1 )	( f(x) = 3 . 2^x )
Graph	A symmetric parabola about the axis of symmetry.	An asymmetric curve with a horizontal asymptote.
Application	Modeling trajectories or areas.	Modeling phenomena of rapid growth or decay, such as compound interest.

Task2:

Provide real world examples of exponential functions and quadratic functions (Minimum 2 for each)that are not discussed in class!

Exponential Functions

Growing a YouTube Channel

If I manage a YouTube channel and I start with 500 subscribers and these subscribers double every month the total number of subscribers N(t) after t months is given by the formula:

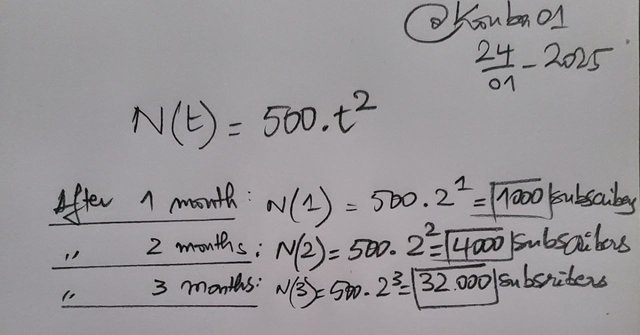
If I continue producing quality content, this exponential growth will allow me to quickly reach a much larger audience.

Radioactive decay

When working with radioactive samples I find that their mass decreases exponentially, for example, for carbon-14 with a half-life of 5730 years, I can use the formula:

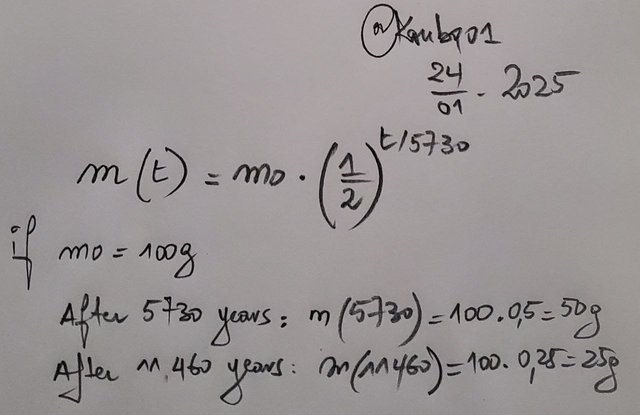
This helps me estimate the age of ancient objects by measuring their carbon-14 content.

Quadratic Functions

Shot of a basketball
When I throw a basketball from an initial height of 2 meters with a velocity of 10 m/s, I can model its height h(t) with the formula:

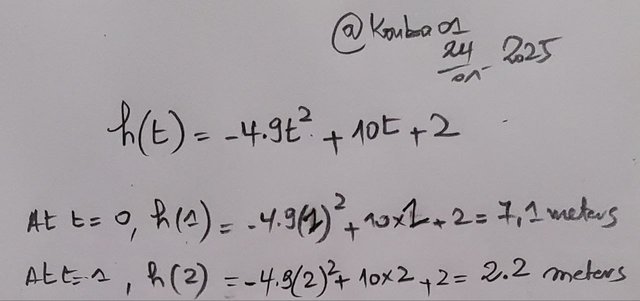
This model lets me predict if the ball will reach the basket.

Construction of a fence

If I want to build a rectangular fence with 40 meters of mesh, I can model the area A(x) as a function of the width x with:

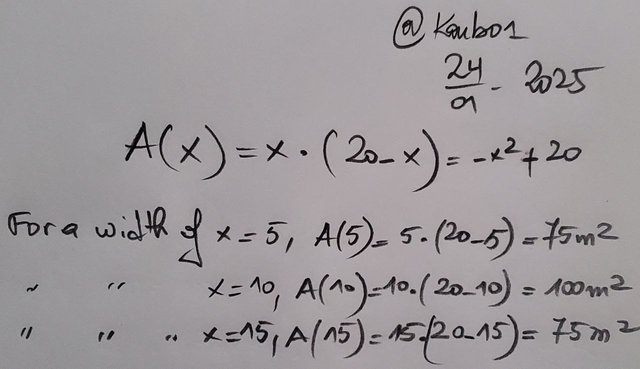
If I want to maximize the area, I need to choose a width of 10 meters, which gives a maximum area of 100^2.

Task3:

Please find out equation of the circle with center (2, 3) and radius 4.

Please solve for x: 2x^2 + 5x - 3 = 0

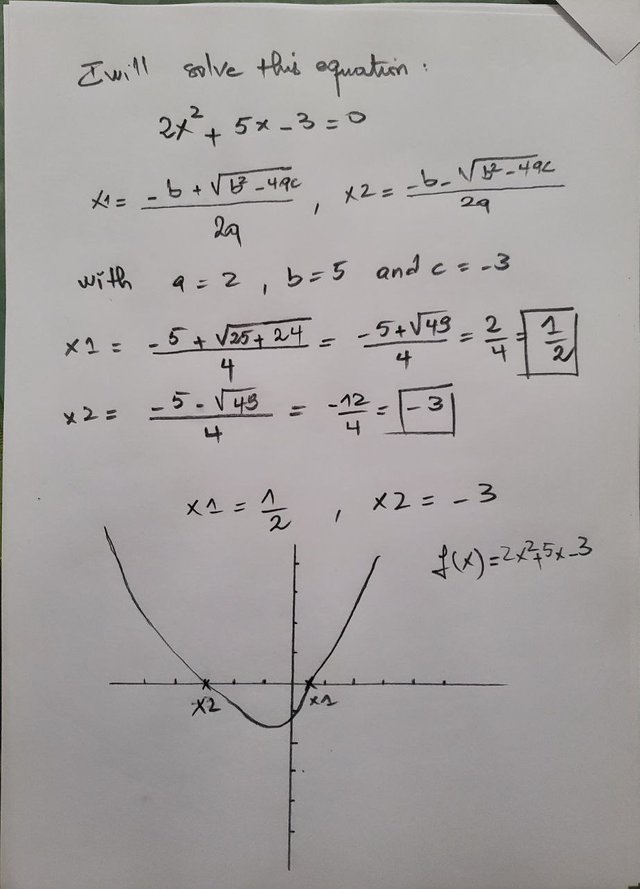
Task4:

Scenario number 1
Suppose there's a satellite dish which is shaped like paraboloid.If equation of the paraboloid is given by y = 0.1x^2 then here x and y are measured in meters so now;

a) You need for graphing this equation.

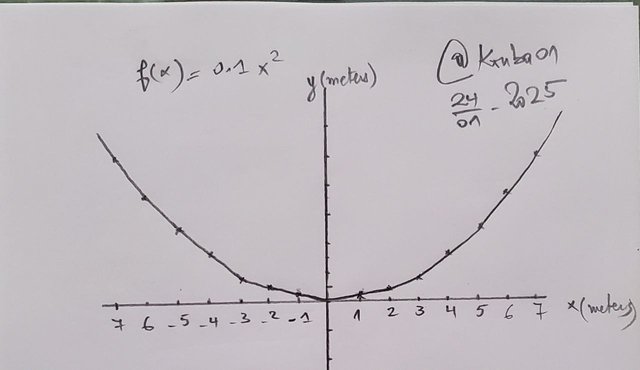
b) You need for finding out focal length of paraboloid.

c) You need for finding out equation of directrix.

Scenario number 2
You need for suppose that there's a ball which is thrown in upward direction from ground with an initial velocity of 50 ft/s.Suppose if height of ball above ground is given by the equation h(t) = -16t^2 + 50t and here t is presenting time in seconds then;

a) You need for graphing this equation.

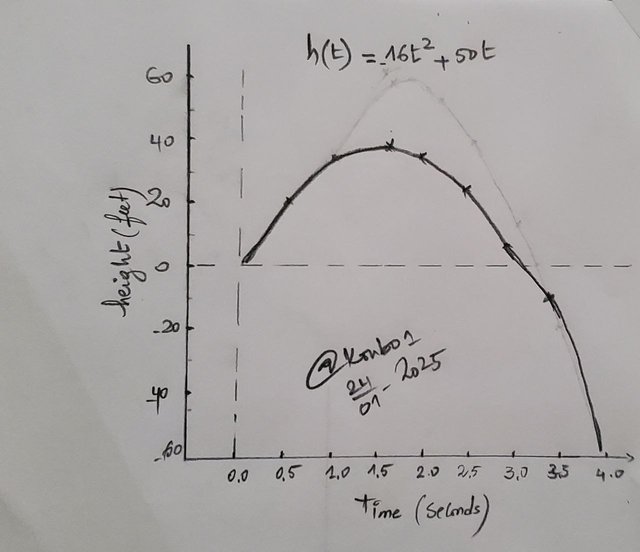
b) You need for finding out maximum height reached by this ball.

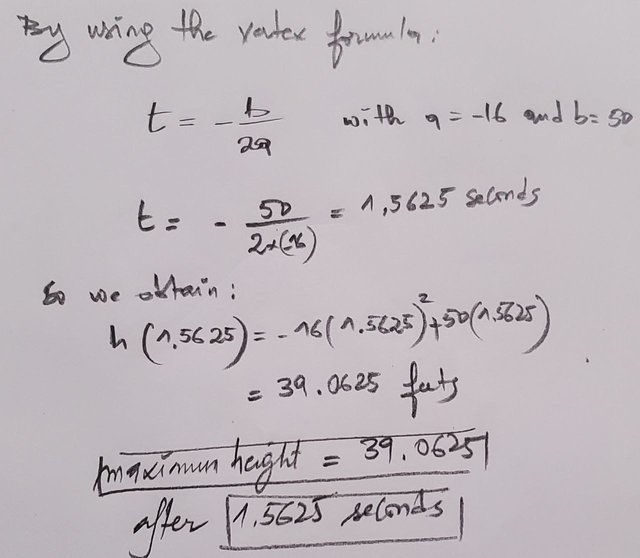
c) You need for finding out time which it is taking for ball for reach to ground.

---

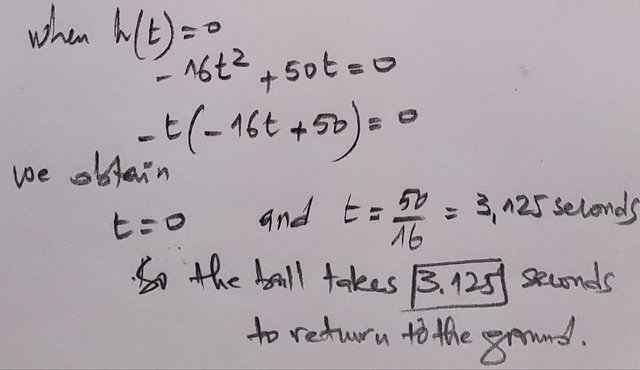
Thank you very much for reading, it's time to invite my friends @graceleon, @adrianagl, @karianaporras to participate in this contest.

Best Regards,
@kouba01