SLC-S22W6//Graphing and conic sections

Hello friends, I'm glad to present my understanding of the concludes class for this week, the class was impactful. Then I'm expected to work and present the below task to prove my understanding.
Without further ado...
| Task 1: |
|---|
Differentiate between quadratic and exponential functions with examples and general forms of each!
| Answer... |
|---|
A quadratic function can said to be a second degree polynomial function, where the the highest power of the variable is 2 and the general form of a quadratic function is the example I'm going to show below...
f(x)=ax2+bx+cf(x)=ax^2+bx+c
where,
a, b, ca, b, c are constants
a ≠ 0a \neq 0 (if not so, it becomes a linear function)
It know that the graph of a quadratic function is a parabola
The parabola here can open upward(a>0a>0)or downward (a<0a< 0)
The vertex is the highest or lowest point depending on the parabola orientation
Remember that the quadratic functions have a constant rate of change in their slope
f(x)=2x2−3x+1f(x)=2x^2-3x+1
This function has a parabola that opens upwards since the a = 2a = 2 which is now positive
an exponential function has a variable in the exponent the general form of an exponential function is below
f( x ) = abxf( x ) = ab^x
where
aa is the initial value
bb is the base (and must be positive and b≠1b \neq 1)
xx is the exponent
The graph of an exponential function is in a curved line
It grows only (if b>1b > 1) or decays (if 0<b<10 < b < 1) rapidly
Exponential functions are often used to model growth and decay processes
f( x ) =3 2xf( x ) = 3 \cdot 2^x
This function has exponential growth since the base b = 2>1b = 2 > 1
| Feature | Quadratic Function | Exponential Function |
|---|---|---|
| General Form | ax2+bx+cax^2+bx+c | abxab^x |
| Graph Shape | Parabola | Curved Line |
| Rate of Change | Constant rate of change in slope | Rapid growth / decay |
| Example | f(x)=2x2−3x+1f(x)=2x^2-3x+1 | f(x)=3 2xf(x)=3 \cdot 2^x |
| Task 2: |
|---|
Provide real world examples of exponential functions and quadratic functions (Minimum 2 for each)that are not discussed in class!
| Answer... |
|---|
Alright, in the below I'm gonna provide the real world example of exponential function and quadratic function that wasn't discussed in class.
Let's check...
If the population of a city is double every 10 years, the growth can be model as my below expression...
P(t)=P0 2t/10P(t) = P_0 \cdot 2^{t/10}
which the P0P_0 is the initial population and tt is time in years
The decay of a radioactive substance can be model as my expression below...
M(t)=M0 e−ktM(t)=M _ 0 \cdot e^{ - kt}
In which the M0M_0 is the initial mass and kk is the decay constant and tt is time
The height of a ball thrown upward is model as the expression below...
h(t)=−16t2+50t+5h(t)=-16t^2+50t+5
In which the tt is time in seconds and h(t)h(t) is the height in feet
If a companys revenue depends on the price of a product it can be model as the expression below...
R(p)=−2p2+50pR(p)=-2p^2+50p
In which the pp is the price of the product and R(p) R(p) is the revenue
| Task 3: |
|---|
Please find out equation of the circle with center (2, 3) and radius 4.
Please solve for x: 2x^2 + 5x - 3 = 0
| Answer... |
|---|
Alright, to solve the above problem I'm going to prevent my solving below on a paper.

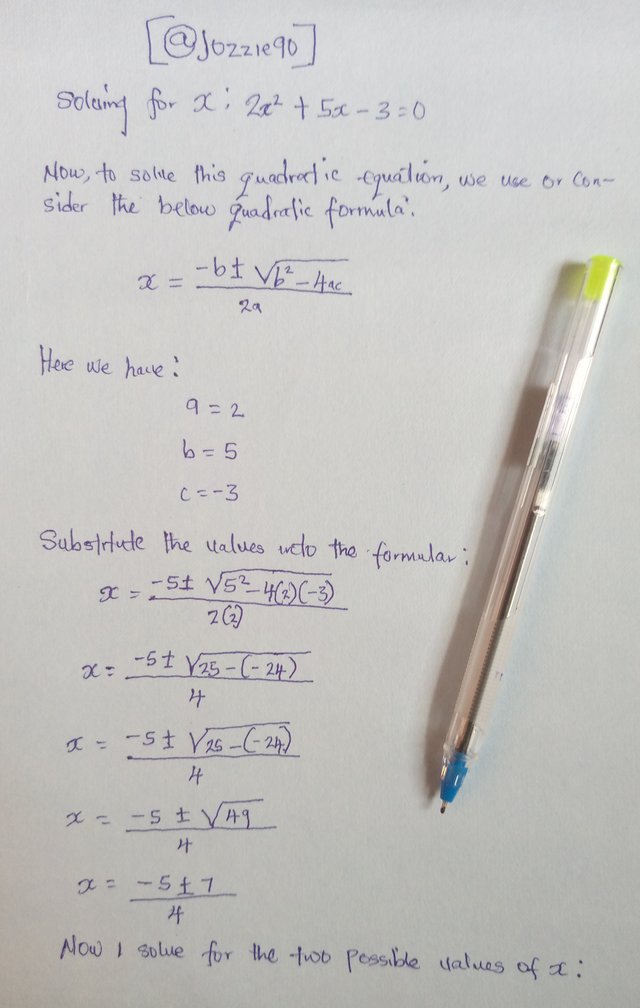
Now gonna solve for two possible value of x:
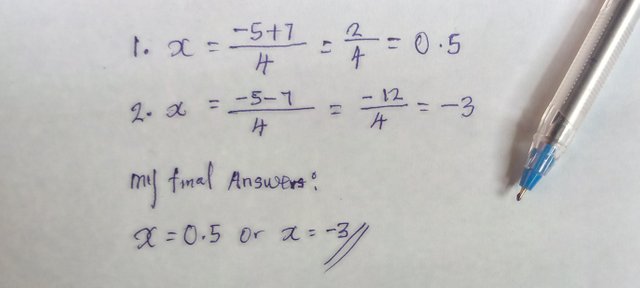
| Task 4: |
|---|
Scenario number 1
Suppose there's a satellite dish which is shaped like paraboloid.If equation of the paraboloid is given by y = 0.1x^2 then here x and y are measured in meters so now;
a) You need for graphing this equation.
b) You need for finding out focal length of paraboloid.
c) You need for finding out equation of directrix.
(Solve the above scenerio based questions and share step by step that how you reach to your final outcome)
| Answer... |
|---|
Senerio 1:
The given equation was as below
y=0.1x2y=0.1x^2
This represents a parabola that opens upwards with the vertex at the origin (0,0) (0, 0) 8n my graph below
➡️ a). Graphing the Equation
To graph the parabola y=0.1x2y=0.1x^2 let's check out on the graph
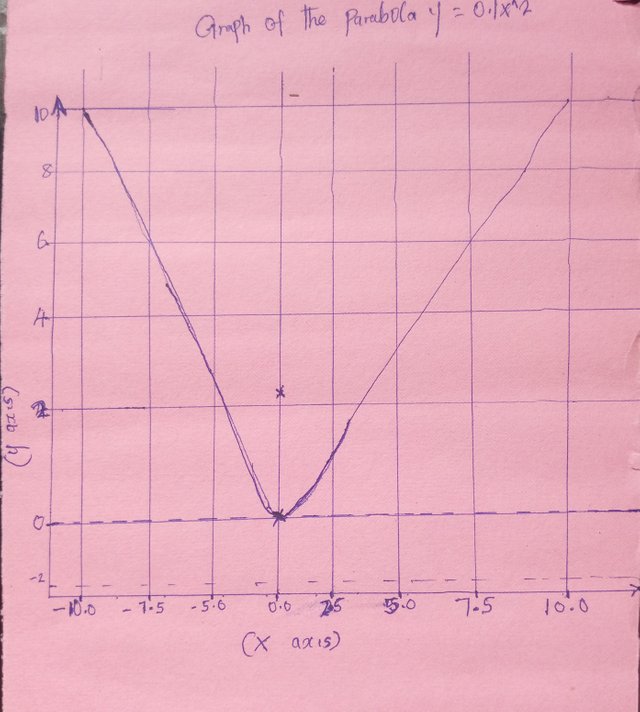 |
|---|
This my graph visually represents the parabola and its focal length and it directri
➡️b.) now, I'm finding the Focal Length
The standard form of the parabola with its vertex at the origin is presented with my calculation below.
 |
|---|
➡️ c) now, I'm finding the Equation of the directrix
the directrix of a parabola is a horizontal line located a distance p
p below the vertex for upward opening parabolas

My final results.
Graph: The parabola
𝑦=0.1x^2
y=0.1x^2
is an upward-opening curve with vertex at
(0,0) (0,0)
The Focal Length: The focal length is 2.5 meters.✅
The directrix: the equation of the directrix is
𝑦=−2.5
y=−2.5✅
Scenario number 2:
You need for suppose that there's a ball which is thrown in upward direction from ground with an initial velocity of 50 ft/s.Suppose if height of ball above ground is given by the equation h(t) = -16t^2 + 50t and here t is presenting time in seconds then;
a) You need for graphing this equation.
b) You need for finding out maximum height reached by this ball.
c) You need for finding out time which it is taking for ball for reach to ground.
| Answer... |
|---|
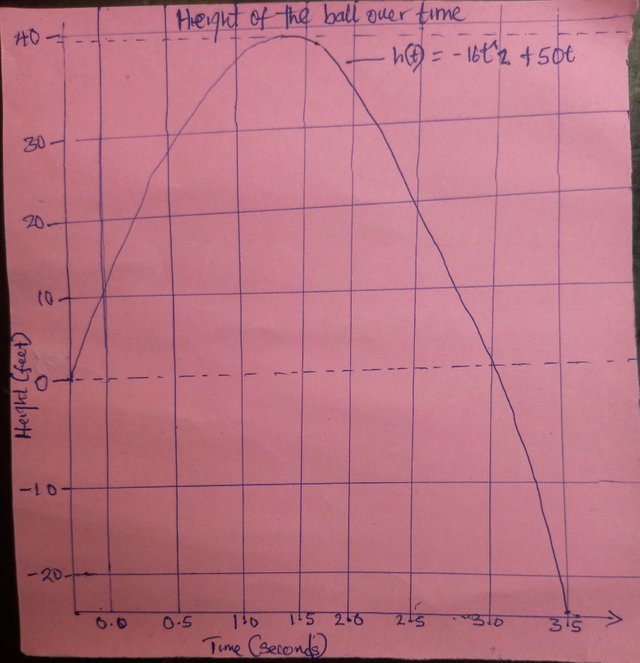
A) Graphing the height equation
The height of the ball as a function of time is given by the equation I'm going to present below...
h(t) = - 16t^2 + 50t
This equation represents a downward opening parabola because the coefficient of t^2 is negative, the graph shows how the height of the ball change with time.
Initially the ball is all the ground (h(0)= 0)
The ball rises, reaches a maximum height and then fall back to the ground
In my gragh:
The x-axis represent time (t) measured in seconds
The y-axis represent height (h(t)) measured in feet
The curve start at (0,0) peaks at the maximum height and return to h =0 when the ball hits the ground
B) finding the maximum height.
To find the maximum height I calculate the vertex of the parabola, the formula for the time at which the vertex occur is as show in my calculation below

C) Time to hit the Ground
The ball hits the ground when the height h(t) become zero
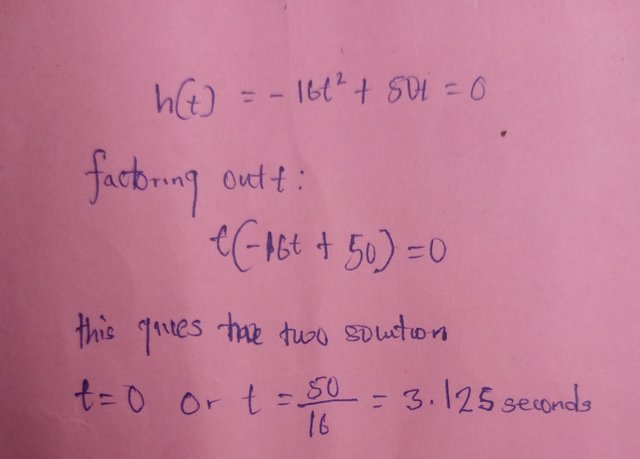
The first solution (t=0) corresponding to the moment the ball is thrown
The second solution ( t= 3.125) is when the ball returns to the ground
So, the Ball takes 3.125 seconds to reach the ground.
My summary answer to A, B and C is :
A) the graph shows the parabolic trajectory of the ball
B) maximum height is 39.06 reached at 1.56 seconds
C) Time to hit the ground is 3.125 seconds
Thank you all for your precious time.
Please permit me to invite @dazzle55, @preshy001 and @samuelnkenta to participate in this learning challenge.

