SLC-S22W5//Polynomial and rational expressions

Greetings Steemit friends

Explain the difference between polynomial and rational expressions. Provide examples of each type of system of equations and describe their general forms.

Both Polynomial and Rational are algebraic expressions, and I will explain the differences between the two.

A polynomial expression consists of variables, constants, and exponents. Polynomials are classified based on the power of the variable and the number of terms. Here you can carry out operations like additions, subtraction, and multiplication. It is not possible to carry the division operation with a variable with Polynomial expression.

General Form

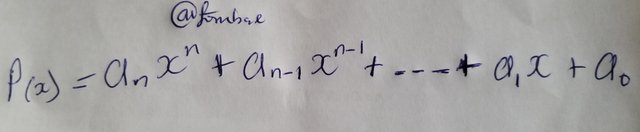
Here an, an-1,. . . a0 are the constant, and n is not a non-negative number.

Examples of Polynomial expression
Constant = 8 ( highest power of the variable is 0)
Quadratic = 3x^2 + 5x -7 ( highest power of the variable is 2)
Cubic = 4x^3 - 2x^2 +x -9 ( highest power of the variable is 3)
Quartic = 2x^4 - x^3 + 4x + 1 ( highest power of the variable is 4)

So you see with a Polynomial expression, the exponents of the variable are nonnegative numbers and the coefficients are constant. Finally, the highest power of the variable gives the degree of the Polynomial.

A rational expression is the fraction of two polynomials, meaning both the numerator and denominator are polynomials. An expression can only be rational if the denominator is not zero(0)

General form

P1(x)
------
P2(x)

Here P1 and P2 are polynomials and P2 cannot be 0.

Examples

1.)

3x^2 + 2x - 5
-----------
x - 4

2.)

x + 1
--------
x^2 - 9

So you can see that rational expression has to do with dividing two polynomials. Since we can divide by zero(0) , the denomination cannot be zero(0).

Explain steps used in simplifying a rational expression. Write some common factors required to be canceled out.

Simplifying a rational expression will mean reducing the expression to the simplest form factoring and canceling the common factors in the numerator and denominator. Let's get an example of a rational expression and apply the steps to simplify.

Expression:

x^2 − 9
------------
x^2 - 6x + 9

Step 1: Start by factoring the numerator and denominator. Here we find the prime factors by factoring out the greatest common factor.

For example a^2 - b^2 = (a - b)(a + b)

x^2 − 9 = (x − 3)(x + 3)

Note that x * x = x^2, 3x - 3x = 0, and -3 * 3 = -9. (You can see (x − 3)(x + 3) is coming from.

​x ^2 - 6x + 9 = (x - 3)(x - 3)

Note that x * x=x^2, -3x - 3x = -6x and -3 * -3 = 9

(x − 3)(x + 3)
-------------
(x - 3)(x - 3)

Step 2: canceling the common factors. Here looking for the common factor between the numerator and denominator. Note that, while canceling the common factor. The denominator should not be equal to 0. In our case, (x−3) which appears in the numerator and denominator will cancel out each other.

(x − 3)(x + 3)
-------------
(x - 3)(x - 3)

We have

(x + 3)
-------
(x - 3)

Step 3: Let's write out simple expressions now

(x + 3)
-------
(x - 3)

We are assuming here that x is not equal to 3. That is for the case of the denominator, because if x = 3. That will mean(3-3) equals 0 when the denominator is not supposed to be zero.

Task 3

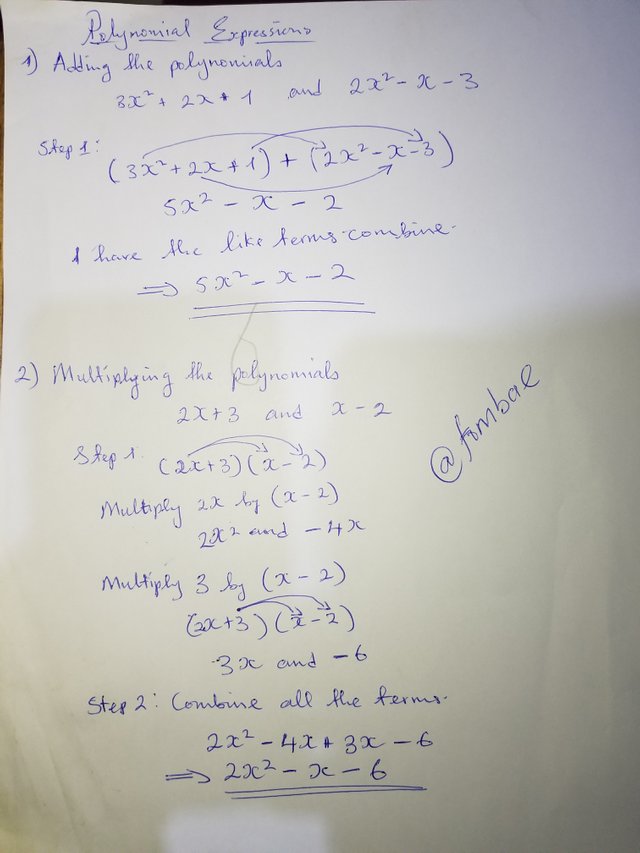
Task 4

Case 1:

Let's break down the problem

• The beads are sold in packets of x
• One packet cost $2
• the beads have a fixed cost of $5
• there is an offer of a 10% discount on the total cost

To write the polynomial expression for representing the total cost (C) of buying x packets.

Therefore, if x represents the packets and one packet costs $2. that will mean

Total cost (C) = $2( x )

Given that there is a fixed cost on beads and not the packet. So no matter the quantity of packets, you have an addition of the fixed cost.

Total cost (C) = 5 + 2( x )

We have the polynomial expression, let's look at how to apply the 10% discount. Discount means reducing the total cost by 10%. So let's look for 10% of the total cost (C)

So, Discount = 10/100 * Total cost (C)

10/100 * 5 + 2( x )
0.10 * ( 5 + 2 x )
= 0.5 + 0.2x

Therefore, applying the discount

C = Total cost (C) - Discount
C = (5 + 2 x ) - (0.5 + 0.2x)

Let's combine the constants

C = (5-0.5) + (2x-0.2x)
c= 4.5 + 1.8x

Polynomial expression for the total cost when the discount applied

C= 4.5 + 1.8x

Let's calculate 5 packets and apply the discount.

x packets = 5 packets

x = 5
C= 4.5 + 1.8x

Let substitute x = 5

C= 4.5 + 1.8(5)
C = 4.5 + 9
C= 13.5

So the total cost for buying 5 packets with a 10% discount
is $13.50

===================

Case 2

Breakdown the problem

Wheat Harvest (WH)= x ton
Barley Harvest (BH)= 3x tons
Total Harvest (TH) = Wheat + Barley
Total Harvest (TH) = x + 3x
Total Harvest (TH) = 4x

Write a rational expression for representing the ratio of wheat to total harvest.

The ratio of Wheat (W) = Wheat Harvest (WH) /Total Harvest (TH)
Ration W = x/4x

Simplify rational expression
x
--
4x

We have to do a calculation in this case

x/4x =1/4

Last section: Calculating ratio for x=4 tone

Wheat Harvest (WH)= 4 ton
Barley Harvest (BH)= 3x tons (3*4 )
Total Harvest (TH) = Wheat + Barley
Total Harvest (TH) = 4 + 12
Total Harvest (TH) = 16

The ratio of wheat = WH /TH
Ratio = 4/16 =1/4

Both ration for wheat to Total Harvest and when the farmer harvests 4 tons of Wheat is 1/4.

---

---

Cheers
Thanks for dropping by
@fombae