SLC-S22W5 // Polynomial and rational expressions
 Diseño en canva.com F
Diseño en canva.com F 
Explicar la diferencia entre expresiones polinómicas y racionales. Proporcionar ejemplos de cada tipo de sistema de ecuaciones y describir sus formas generales.
💠 Expresiones polinómicas
Las expresiones polinómicas son expresiones algebraicas que se caracterizan por contener un conjunto finito de términos cuyas variables tienen potencias enteras positivas y coeficientes o constantes que les multiplican, de tal manera que dichos términos operan aritméticamente entre sí a través de la suma, resta y multiplicación.
Se diferencian de las expresiones racionales en que carecen de una expresión polinómica como denominador.
♦ Forma general de las expresiones polinómicas.
Las expresiones polinómicas pueden tener una o más variables. Los polinomios de una variable tienen la forma:
P(x) = anxn + an-1xn-1 + …+ a1x1 + a0x0
Donde,
“x” es la variable
“n” es el grado del polinomio que corresponde al mayor exponente de la variable
“a0,…, an” son los coeficientes del polinomio.
“P” es un polinomio de grado “n” en la variable “x”
Los polinomios de varias variables, obviamente tienen en total más de una variable.
♦ Ejemplos de expresiones polinómicas.
P(x) = 5, es un polinomio de grado 0 o término independiente.
P(x) = 4x+2 , es un polinomio de grado 1 en la variable "x".
P(x) = x2 + y - 1, es un polinomio de grado 2 en la variable "x" y de grado 1 en la variable "y".
P(x) = x3-y + z, es un polinomio de grado 3 en la variable "x" y de grado 1 en la variable "y" y "z".
♦ Representación gráfica.
A continuación podemos ver una gráfica de la expresión polinómica como ejemplo: 2x3 + 5x2
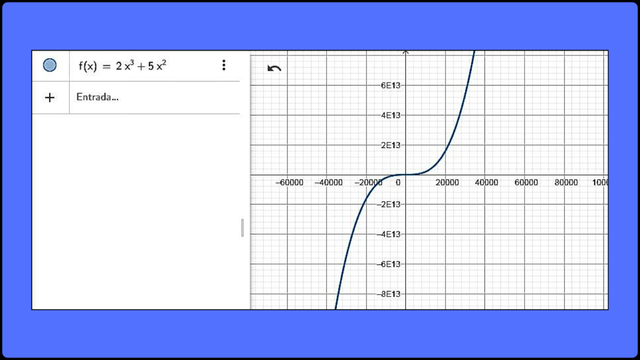 Ejemplo de representación gráfica de la expresión 2x3 + 5x2 F
Ejemplo de representación gráfica de la expresión 2x3 + 5x2 FEs una expresión polinómica de grado 3 en la variable "x".
💠 Expresiones racionales
Las expresiones racionales son relaciones o cocientes entre dos expresiones polinómicas. Es decir, son fracciones algebraicas cuyo numerador y denominador son expresiones polinómicas. Por tanto, el denominador no puede ser nulo o cero.
♦ Forma general de las expresiones racionales.
P(x) / Q(x)
Donde,
P(x) es el polinomio del numerador.
Q(x) es el polinomio del denominador y debe diferente de cero (0).
♦ Ejemplos de expresiones racionales.
1/x
(x-1)/(x-6)
(x2+5)/(2x+1)
♦ Representación gráfica.
A continuación podemos ver una gráfica de la expresión racional como ejemplo: (x-1)/(x-6)
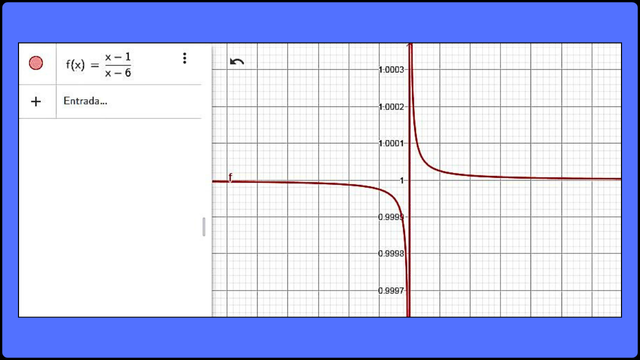 Ejemplo de representación gráfica de la expresión racional (x-1)/(x-6) F
Ejemplo de representación gráfica de la expresión racional (x-1)/(x-6) F 
Explica los pasos usados en la simplificación de una expresión racional. Escribe algunos factores comunes requeridos para ser anulados.
Para simplificar una expresión racional, es fundamental que cada polinomio pueda ser factorizado. Al transformar las expresiones del numerador y el denominador a través de la factorización se pueden eliminar, cancelar o anular factores comunes. En tal sentido, los factores comunes que se dividen entre sí son iguales a uno.
En tal sentido, para simplificar una expresión racional se deben seguir los siguientes pasos:
- Factorizar el numerador y el denominador cuando esto sea posible.
- Comparar los resultados y simplificar los factores comunes.
- Se debe tener en cuenta, desde el inicio de la factorización, el valor de la variable para el cual el denominador se hace cero (0), pues es un punto de crítico o de discontinuidad en la expresión original que desaparece luego de simplificar los factores comunes.
Simplificar la expresión racional: (x2 - 6x + 8) / (x - 2)
- Se factoriza el numerador y tenemos:
(x - 4)(x - 2) / (x - 2) - Se comparan las expresiones y se simplifica el factor común:
(x - 4)(x - 2) / (x - 2) - El resultado es:
x - 4
El resultado se puede ver gráficamente como sigue:
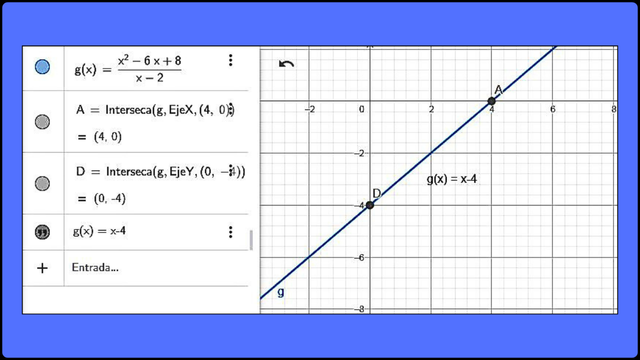 Representación gráfica de la expresión racional (x2 - 6x + 8) / (x - 2) F
Representación gráfica de la expresión racional (x2 - 6x + 8) / (x - 2) F Como se puede observar, el resultado es una línea recta g(x) = x – 4, lo que valida el resultado obtenido en la simplificación.
En importante advertir que si se trata de la operación de varias expresiones racionales, se deben seguir las mismas reglas básicas para operar las fracciones aritméticas o numéricas. Por tanto, la simplificación es más compleja que la solicitada en esta tarea. En estos casos, recomiendo seguir los siguientes pasos:
Suma y resta de fracciones
- Encontrar el mínimo común múltiplo entre los denominadores, es decir, se seleccionan los factores comunes y no comunes con su mayor exponente.
- Además de sumar y restar, el numerador debe multiplicarse, combinarse y refactorizarse comúnmente para demostrar que se ha reducido adecuadamente a la expresión más simple posible.
- Como resultado de la suma se obtiene una expresión racional que debe simplificarse siguiendo el procedimiento previamente explicado.
- Indicar los puntos críticos donde los valores de la variable hacen que el denominador o denominadores sean cero (0).
Sumar las expresiones racionales: (x-1) / x + (x-2) / (x-1)
- Determinar el mínimo común (m.c.m.) múltiplo entre los denominadores y tenemos el denominador resultante: (x)(x-1)
- Se define el numerador como en las fracciones numéricas, multiplicando la primera fracción por el m.c.m. dividido por su denominador, luego sumamos el producto de la segunda fracción por el m.c.m. divido por su denominador:
[ (x-1) / x ] (x)(x-1) + [ (x-2) / (x-1) ] (x)(x-1)
(x-1)(x-1) + (x-2)(x) - Se obtiene la siguiente expresión racional:
[ (x-1)(x-1) + (x-2)(x) ] / [ (x)(x-1) ] - Desarrollando las operaciones en el numerador tenemos:
[ (x2 - 2x +1 + x2 - 2x ] / [ (x)(x-1) ]
(2x2 - 4x +1) / [ (x)( x-1) ], factorizamos x en el numerador
[ (x)(2x - 4 +1/x) ] / [ (x)(x-1) ] - El resultado simplificado es:
(2x - 4 +1/x) / (x-1)
El resultado se puede ver gráficamente como sigue:
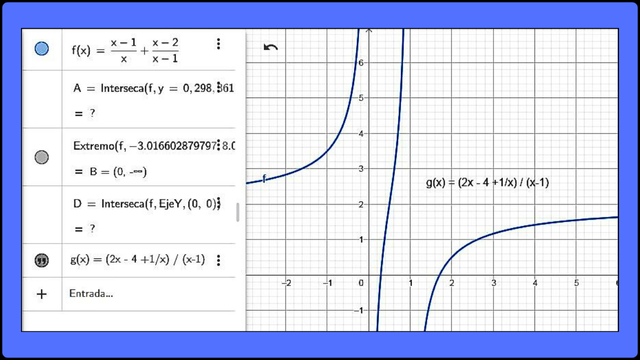 Representación gráfica de la expresión racional (x-1) / x + (x-2) / (x-1) F
Representación gráfica de la expresión racional (x-1) / x + (x-2) / (x-1) FComo se puede observar, el resultado es una función g(x) = (2x - 4 +1/x) / (x-1) que tiene discontinuidades en x=0 y x=1, lo que valida el resultado obtenido en la simplificación.
Multiplicación de expresiones racionales.
- Realizar el producto directo entre los numeradores y denominadores.
- Factorizar los numeradores y denominadores.
- Eliminar factores comunes.
- El resultado se expresa comúnmente factorizado para demostrar que se ha reducido adecuadamente a la expresión más simple posible.
- Indicar los puntos críticos donde los valores de la variable hacen que el denominador o denominadores sean cero (0).
Multiplicar las expresiones racionales: [ (x2 + x) / (x2-1) ] [ (2x + 4) / (x + 2)2 ]
- Se factorizan el numerador y denominador:
[ x(x + 1) / (x - 1)(x + 1) ] [ 2(x + 2) / (x + 2)(x + 2) ] - Se eliminan factores comunes:
[ x(x + 1) / (x - 1)(x + 1) ] [ 2(x + 2) / (x + 2)(x + 2) ]
[ x / (x + 1) ] [2 / (x + 2) ] - Se hace el producto directo entre numeradores y denominadores, obteniéndose el resultado simplicado:
2x / [ (x + 1) (x + 2) ]
El resultado se puede ver gráficamente como sigue:
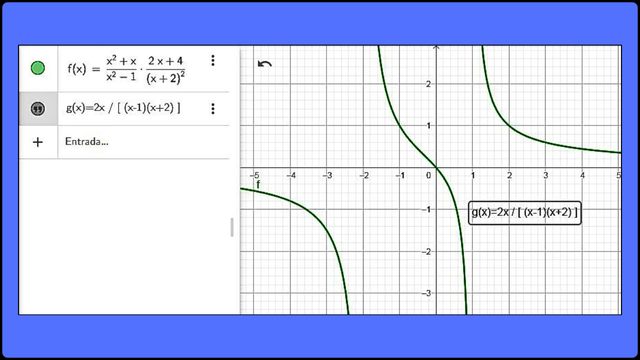 Representación gráfica de la expresión racional [ (x2 + x) / (x2-1) ] [ (2x + 4) / (x + 2)2 ] F
Representación gráfica de la expresión racional [ (x2 + x) / (x2-1) ] [ (2x + 4) / (x + 2)2 ] FComo se puede observar, el resultado es una función g(x) = 2x / [ (x + 1) (x + 2) ] que tiene discontinuidades en x= ±1 y x= -2, lo que valida el resultado obtenido en la simplificación.
División de expresiones racionales
Esta operación consiste es convertir el problema de división en una multiplicación siguiendo la regla básica de la división de fracciones numéricas (regla de la “doble C”). A partir de allí proceder como en la multiplicación de expresiones racionales indicadas anteriormente.
- Multiplicamos el numerador de la primera fracción por el denominador de segunda fracción y obtenemos el numerador resultante. De igual manera, multiplicamos el denominador de la primera fracción por el denominador de la segunda y obtenemos el denominador resultante.
- Factorizar el numerador y denominador resultantes.
- Eliminar factores comunes.
- El resultado se expresa comúnmente factorizado para demostrar que se ha reducido adecuadamente a la expresión más simple posible.
- Indicar los puntos críticos donde los valores de la variable hacen que el denominador o denominadores son cero (0).
Dividir las expresiones racionales: [ (x2 + x - 2) / (x - 1) ] ÷ [ (x + 2) / (x - 2) ]
[ (x2 + x - 2)(x - 2) ] ÷ [ (x + 2)(x - 1) ]
[ (x - 1)(x + 2)(x - 2) ] ÷ [ (x + 2)(x - 1) ]
[ (x - 1)(x + 2)(x - 2) ] ÷ [ (x + 2)(x - 1) ]
x - 2
Hemos eliminado los factores comunes, podemos observar que los denominadores se anulan en x = 1 y x= ±2, los cuales son puntos de discontinuidad de la expresión racional original.
El resultado se puede ver gráficamente como sigue:
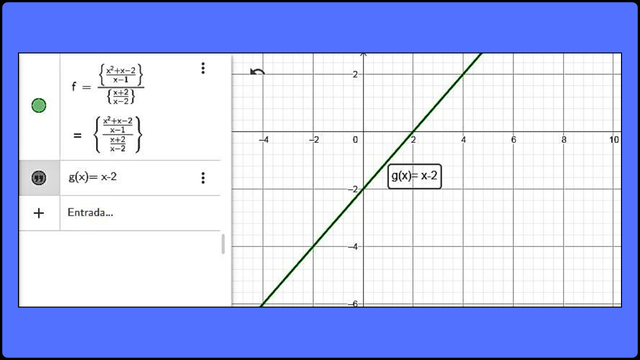 Representación gráfica de la expresión racional [ (x2 + x - 2) / (x - 1) ] ÷ [ (x + 2) / (x - 2) ] F
Representación gráfica de la expresión racional [ (x2 + x - 2) / (x - 1) ] ÷ [ (x + 2) / (x - 2) ] F Como se puede observar, el resultado es una función g(x) = x - 2 que tiene discontinuidades en x= 1 y x= ±2, lo que valida el resultado obtenido en la simplificación.

Por favor, suma estas expresiones polinómicas (3x2 + 2x + 1) y (2x2 - x - 3) y comparte tu expresión final.
- Tenemos: (3x2 + 2x + 1) + (2x2 - x – 3)
- Agrupamos términos del mismo grado:
(3x2 + 2x2) + (2x - x) + (1 - 3) - Resolvemos las sumas y las restas:
(3 + 2)x2 +(2 - 1)x +(1 - 3)
5x2 + x - 2
 Suma de las expresiones polinómicas (3x2 + 2x + 1) + (2x2 - x – 3)
Suma de las expresiones polinómicas (3x2 + 2x + 1) + (2x2 - x – 3)Con lo que hemos aprendido en el curso podemos resolver esta ecuación cuadrática hallando las raíces para facilitar su representación gráfica como sigue:
Aplicamos la fórmula general de resolución de una cuadrática:
x = [-b ± √(b2-4ac)] / (2a)
donde, a = 5; b = 1; c = - 2, por tanto sustituimos y operamos matemáticamente:
x = [ -1 ± √(12-4(5)(-2) ] / (2(5)), simplificando tenemos:
x = [ -1 ± √(1 + 40) ] / 10, simplificando el paréntesis
x = [ -1 ± √(41) ] / 10, simplificando la fracción
x = -1/10 ± √41 / 10, calculamos las fracciones
x = -0.10 ± 0.64
La raíces son:
x1 = -0.10 - 0.64 = - 0.74
x2 = -0.10 + 0.64 = 0.54
Por tanto, se ubican en los puntos A(-0.74;0) y B(0.54;0) en un plano cartesiano.
Otros puntos de interés para la gráfica de la función son:
- El extremo de la curva para x= -b / (2a) = -1 / 10 = -0.10
Se sustituye el valor de x en la función y tenemos:
f(-0.10) = 5(-0.10)2 +(-0.10) - 2 = -2.05.
Por tanto, el extremo se ubica en el punto C(-0.10; -2.05) - El corte en la ordenada para x =0, sustituimos en la función y tenemos:
f(0) = 5(0)2 +(0) - 2 = -2.
Por tanto, el corte en la ordenada se ubica en el punto D(0; -2)
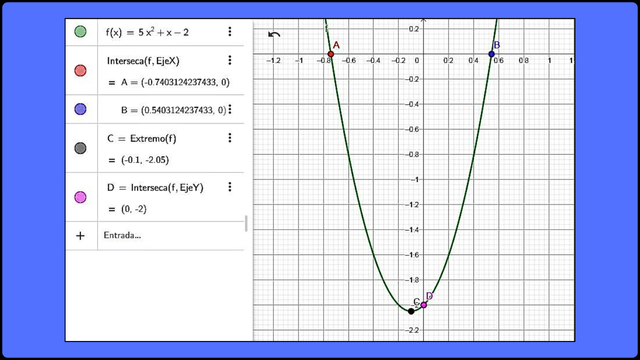 Representación gráfica de la expresión 5x2 + x - 2
F
Representación gráfica de la expresión 5x2 + x - 2
FComparte la multiplicación de expresiones polinómicas (2x + 3) y (x - 2) con el resultado final de la expresión resultante.
- Tenemos: (2x + 3)(x - 2)
- Aplicamos la propiedad distributiva: (2x)(x) +(2x)(-2) +(3)(x) + (3)(-2)
- Resolvemos los productos planteados: 2x2 - 4x + 3x - 6
- Sumamos y restamos términos del mismo grado: 2x2 - x - 6
2x2 - x - 6
 Producto de expresiones polinómicas (2x + 3)(x - 2)
Producto de expresiones polinómicas (2x + 3)(x - 2)Como procedimos en el ejemplo ejercicio anterior hallamos las raíces de la función para facilitar su representación gráfica como sigue:
Aplicamos la fórmula general de resolución de una cuadrática:
x = [-b ± √(b2-4ac)] / (2a)
donde, a = 2; b = -1; c = - 6, por tanto sustituimos y operamos matemáticamente:
x = [ 1 ± √(12-4(2)(-6) ] / (2(2)), simplificando tenemos:
x = [ 1 ± √(1 + 48) ] / 4, simplificando el paréntesis
x = [ 1 ± √(49) ] / 4, simplificando la expresión
x = 1/4 ± 7 / 4, calculamos las fracciones
x = 0.25 ± 1.75
La raíces son:
x1 = 0.25 – 1.75 = - 1.50
x2 = 0.25 + 1.75 = 2.00
Por tanto, se ubican en el punto A(-1.50;0) y B(2;0) en un plano cartesiano.
Otros puntos de interés para la gráfica de la función son:
- El extremo de la curva para x= -b / (2a) = 1 / 4= 0.25
Se sustituye el valor de x en la función y tenemos:
f(0.25) = 2(0.25)2 -(0.25) - 6 = -6.13.
Por tanto, el extremo se ubica en el punto C(-0.10; -2.05) - El corte en la ordenada para x =0, sustituimos en la función y tenemos:
f(0) = 2(0)2 -(0) - 6 = -6.
Por tanto, el corte en la ordenada se ubica en el punto D(0; -6)
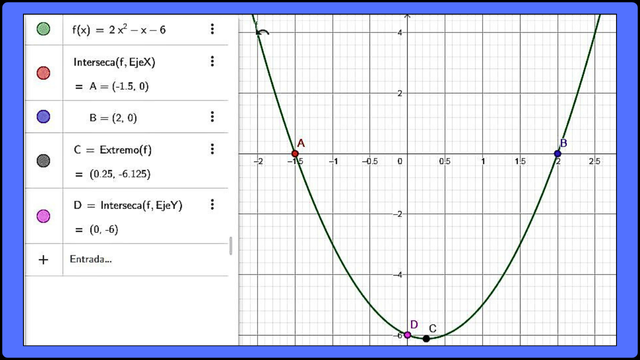 Representación gráfica de la expresión 2x2 - x - 6
F
Representación gráfica de la expresión 2x2 - x - 6
F
Supongamos que una persona llamada Ali tiene una tienda de artesanía y vende bisuterías en x paquetes que tienen un coste fijo de 5 $ más 2 $ por cada paquete. Ahora tienes que escribir una expresión polinómica para representar el costo total (C) de comprar x paquetes de bisuterías considerando que hay un descuento del 10%. También tienes que calcular el costo total si Ali compra 5 paquetes de bisutería.
Primero vamos a identificar los datos del enunciado:
- C es el costo total de la compra que depende del número de paquetes. Es decir, es una función de la forma C(x).
- x representa el número de paquetes de la compra.
- El costo de cada paquete son 2$. Es decir, 2x
- El costo fijo de 5$ es un valor constante para cualquier cantidad de paquetes involucrados en la compra. Es decir, 5.
- Se determina entonces que el costo de la oferta normal, sin descuento, es la suma de los 2$ por paquete y el costo fijo 5$. Es decir, 2x + 5.
- Cuando se considera un descuento (d) se aplica sobre el costo de la oferta normal, como se hace en el comercio real. Es decir, d(2x + 5)
- Determinar la expresión polinómica del costo total considerando un descuento del 10%
- Determinar el costo de compra de Alí por 5 paquetes
En base a estos datos, podemos deducir que el costo total C(x) es igual a la suma del costo por paquete y el costo fijo menos el descuento, lo cual se puede expresar de la siguiente manera:
C(x) = (2x + 5) - d(2x+5)
Factorizando la expresión: C(x) = (2x+5)(1 - d)
C(x) = (2x+5)(1 - d)
[ Es la expresión polinómica general del costo total ]
Donde,
“C(x)” es la función que representa el costo total dependiente de “x”
“x” es la variable que representa la cantidad de paquetes a comprar
“d” es el descuento a aplicar por la compra
“2,1 y 5” son valores constantes
Para encontrar la expresión polinómica del costo total de compra que considera un 10% de descuento, basta con sustituir el valor del descuento (d) igual a 0.10 en esta expresión general como sigue:
Tenemos: C(x) = (2x + 5)(1- d)
Sustituimos d = 0.10 y tenemos:
C(x) = (2x + 5)(1- 0.10), luego simplificamos y obtenemos:
C(x) = (2x + 5)(0.90) = 1.80x + 4.50
C(x) = 1.80x + 4.50
[Es la expresión polinómica que representa el costo total de compra de “x” paquetes “C(x)” considerando un 10% de descuento].
Gráficamente se puede representar a continuación:
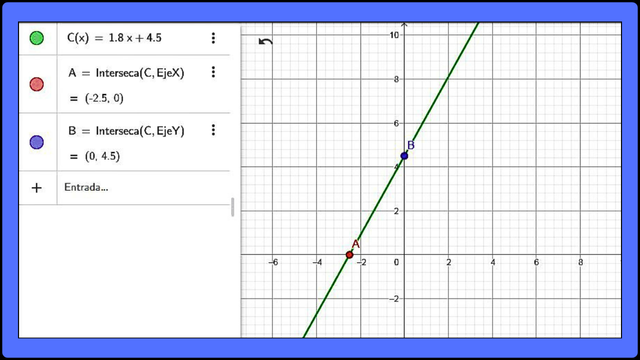 Representación gráfica de la expresión 1.80x + 4.50
F
Representación gráfica de la expresión 1.80x + 4.50
FTambién se pide calcular el costo total, si Alí compra 5 paquetes de bisutería. Es decir, que x = 5. En este caso, tendría dos condiciones a evaluar:
- Costo total sin descuento (d = 0%)
- Costo total con descuento (d = 10%)
- Costo total sin descuento (d = 0%)
Utilizamos la expresión polinómica general:
C(x) = C(x) = (2x + 5)(1- d)
Luego sustituimos x = 5 y d = 0
C(5) = (2)(5) + 5 = 10 + 5 = 15
Por tanto, el costo total de la compra de 5 paquetes es igual a 15$ sin tomar en cuenta el descuento. - Costo total con descuento (d = 10%)
Utilizamos la expresión polinómica:
C(x) = 1.80x + 4.50
Luego sustituimos x = 5 y d = 0.10
C(5) = 1.80(5) + 4.50 = 9 + 4.50 = 13.50
Por tanto, el costo total de la compra de 5 paquetes es igual a 13.50 $ tomando en cuenta un descuento del 10%.
En conclusión, si Alí compra 5 paquetes de bisutería pagaría 15 $ y con el descuento del 10% pagaría 13.50 $. Efectivamente se demuestra que si el costo sin descuento son 15$ y aplicamos el descuento del 10%(15$) = 1.5$, entonces tenemos 15$ - 1.5$ = 13.5$, lo que valida el resultado obtenido y las expresiones polinómicas determinadas.
 Resolución del escenario 1
Resolución del escenario 1💠 Escenario número 2.
Supongamos que hay un agricultor que cosecha x toneladas de trigo y 3x toneladas de cebada. Ahora necesitas escribir una expresión racional para representar la relación entre el trigo y la cosecha total en la que hay trigo y cebada y tienes que simplificar la expresión también al final. También necesitas calcular la relación entre el trigo y la cosecha total si el agricultor está cosechando 4 toneladas de trigo.
Primero identificamos los datos del enunciado:
- Tenemos que “x” son las toneladas de cosecha de trigo
- La cosecha de cebada triplica las de trigo, es decir, son 3x
- Tenemos que la cosecha total es la cosecha de trigo + la cosecha de cebada
- Se pide la expresión racional de la relación entre trigo y cosecha total
- Se pide la relación entre trigo y cosecha total cuando la cosecha de trigo es 4 toneladas
En base a estos datos, deducimos la expresión racional solicitada entre el trigo y la cosecha total como sigue:
Cosecha de trigo / Cosecha total
donde,
Cosecha de trigo = x
Cosecha de cebada = 3x
Cosecha total = Cosecha de trigo + Cosecha de cebada = (x + 3x)
Sustituyendo en la expresión de la relación tenemos:
x / (x + 3x ) = x/(4x), luego simplificamos y obtenemos:
1/4 ó 0.25
Por tanto, la expresión racional entre el trigo y la cosecha total es una constante igual a 1/4 ó 0.25. Esto significa que el trigo ocupa una cuarta parte ó 25% de la cosecha total. Es decir, que por cada tonelada de cosecha de trigo se cosecha un total de 4 toneladas en las que hay trigo y cebada.
Por otro lado, nos preguntan por la relación trigo/cosecha total cuando se cosechan 4 toneladas de trigo.
Como demostramos anteriormente la relación trigo/cosecha total es una constante igual a 1/4 ó 0.25. Por tanto, no varía con la cantidad cosechada de trigo. Esto lo puedo demostrar a través del mismo razonamiento que llevó a esa conclusión como sigue:
Si x = 4 ton, tenemos:
Cosecha de trigo = x =4
Cosecha de cebada = 3x = 3(4) = 12
Cosecha total = Cosecha de trigo + Cosecha de cebada = (x + 3x) = 4+12 = 16
La relación entre el trigo y la cosecha total viene expresada como:
Cosecha de trigo/Cosecha total = 4/16 = 1/4 ó 0.25
Por tanto, la relación entre la cosecha de trigo y la cosecha total es de 1/4 ó 0.25 si el agricultor cosecha 4 toneladas de trigo. Esto significa que la cosecha de trigo representa una cuarta parte ó 25% de la cosecha total. Por tanto, si el agricultor cosecha 4 toneladas de trigo, la cosecha total es 4 veces mayor, es decir (4)(4) = 16 toneladas.
 Resolución del escenario 2
Resolución del escenario 2
Saludos a @khursheedanwar
Notas:
📌 Imágenes presentadas con la aplicación canva.com
📌 Invito a participar a mis amigos @patjewell @paholags @marito74 @genomil @dasudi @dove11 @goodybest
📌 Más información del concurso en el siguiente enlace.
📌 Mi twitter: steemit_casv
📌 Invito a participar a mis amigos @patjewell @paholags @marito74 @genomil @dasudi @dove11 @goodybest
📌 Más información del concurso en el siguiente enlace.
📌 Mi twitter: steemit_casv
¡Gracias por su visita!

Post compartido en X.com:
https://x.com/steemit_casv/status/1881077894958694582
Saludos cordiales.