SLC-S22W4 | Ecuaciones Lineales y Ecuaciones Cuadráticas
Saludos amigos steemians.

Las ecuaciones lineales y cuadráticas son herramientas matemáticas fundamentales para resolver problemas en la vida cotidiana, la economía, la física, la ingeniería y el diseño. Es por ello que resulta importante conocer los distintos métodos de resolución de la forma en la que se pueden emplear en la cotidianidad.
Explicar la diferencia entre ecuaciones lineales y cuadráticas. Proporcionar ejemplos de cada tipo de sistema de ecuaciones y describir sus formas generales.
Una Ecuación Lineal, es aquella donde el exponente más alto en las variables dadas es 1, por lo que su representación gráfica viene dada por una línea recta.
Su forma general es: ax+b=c, donde a se llama el coeficiente de x, b y c son coeficientes constantes. Por ejemplo:
- 3x + 6 = 12
Realizando la representación gráfica de ello sería:
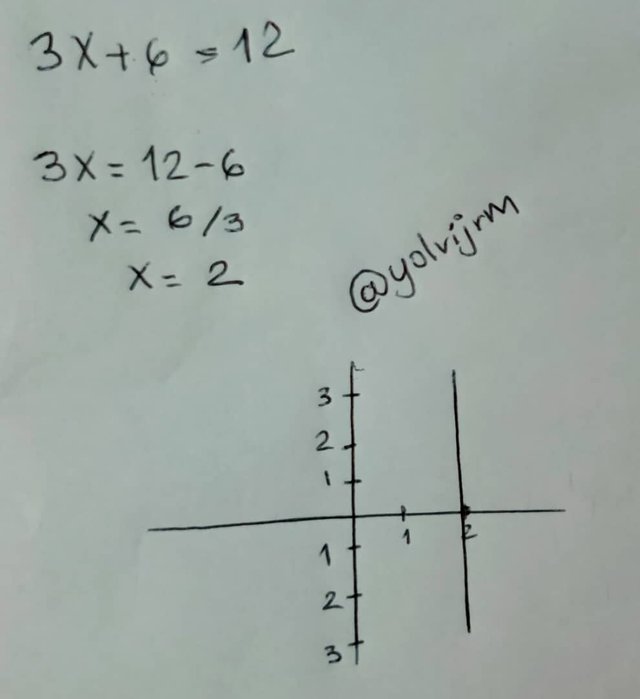
Un ejemplo práctico sería ua sala de juegos, donde el alquier de cada máquina tiene una tarifa inicial de 5 $ + 2 $ por hora. Si una persona alquila una paga 80$ por el alquiler de una de estas máquinas, entonces el número de horas viene dado por:
2x + 5 = 80
Pror otro lado, cuando se habla de Ecuación Cuadrádica, se hace referencia a aquella ecuación de de segundo grado, es decir que su variable está elevada al la potencia 2, y su representación gráfica viene dada por una parábola.
Su forma general es: ax² + bx + c = 0; donde a, b y c son constantes y a tiene que ser diferente de 0. Por ejemplo:
x² - 4x + 3 = 0
Realizando una representación gráfica de ello, sería:
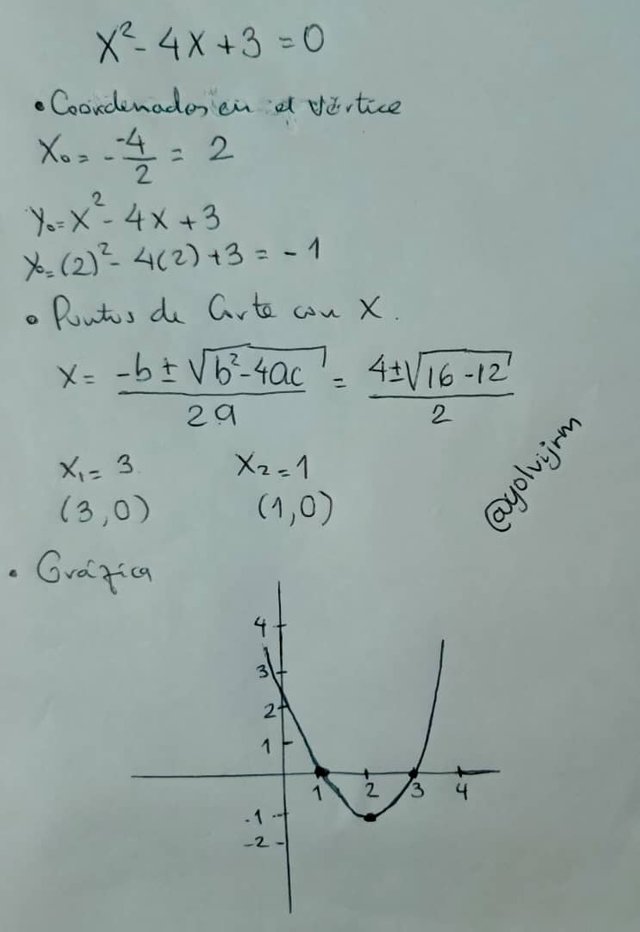
Un ejemplo práctico de ello sería una empresa que prepara pizzas, y el costo (c) de preparar x unidades viene dado por:c = x² + 3x + 120
Esta ecuación expresa el costo de producción, donde x² es el costo de los materiales, 3x es el costo de la mano de obra y 120 (el término constante) es el costo fijo.
En síntesis, a continuación se presenta un resumen de las principales diferencias entre las ecuaciones lineales y las ecuaciones cuadráticas.
| Ecuaciones Lineales | Ecuaciones Cuadráticas |
|---|---|
| Su mayor potencia es 1 | Su mayor potencia es 2. |
| Su gráfico es una línea recta | Su gráfico es una parábola |
| Se resuelven con operaciones algebraicas primarias como suma, resta, multiplicación y división. | Se resuelve por medio de métodos como la fórmula cuadrática, completación de cuadrado, factorizando y graficas. |
| Solo tiene una solución. | Puede tener dos soluciones separadas, una solución repetida o ninguna solución real. |
Describir métodos para resolver ecuaciones cuadráticas y compartir pros y contras de cada método.
Para hallar la solución de las ecuaciones cuadráticas se conocen cuatro métodos básicos: Factorización, completación de cuadrados, fórmula general y el método gráfico.
1.- Factorización:
Factorizar es expresar un número o expresión algebraica como el producto de otros números (o términos) menores por los cuales este se puede dividir. En las ecuaciones cuadráticas se debe hallar dos expresiones que al multiplicarse den como resultado la ecuación de segundo grado. Cada uno de los términos algebraicos se iguala a cero para despejar a la incógnita.
Por ejemplo: x² - 7x + 10 = 0. Para factorizar, se debe hallar dos números que multiplicados den 10 y que sumados den -7; este par de números serán -5 y -2.
Los factores tendrán en común a la x:
x² - 7x + 10 = (x - 5) (x - 2).
Ahora se iguala a cero cada factor, y se despeja la incógnita en cada caso
(x - 5) = 0
x = 5(x - 2) = 0
x = 2
| Ventajas | Desventajas |
|---|---|
| Manera rápida y veloz de resolver ecuaciones cuadráticas simples | No siempre aplicable, algunas ecuaciones cuadráticas no se pueden factorizar |
| Proporciona una base sólida para comprender otros conceptos algebraicos. | Podría ser complejo en casos de cuadráticas complejas. |
2.- Completación de Cuadrados.
Este método consiste en transformar la ecuación ax²+bx + c = 0 en un trinomio cuadrado perfecto, lo que significa un trinomio con dos términos cuadráticos y un término que sean el doble producto de los términos.
Por ejemplo: 5x² + 6x −8 = 0 .
Primeramente se ivide los términos de la ecuación entre el coeficiente de x², en este caso entre 5.
(5x²)/5 + (6x)/5 −(8)/5
Se despeja el término constante de la ecuación, en este caso – 8/5.
x² + (6/5)x = 8/5
Ahora se divide el coeficiente de x entre 2, luego eleva al cuadrado este cociente y se suma en ambos miembros de la ecuación:
(6/5) / 2 = 3/5
(3/5)² = 9/25
x² + (6/5)x + 9/25 = 8/5 + 9/25
x² + (6/5)x + 9/25 = 49/25
El trinomio.
x² + (6/5)x + 9/25
Es cuadrado perfecto y su factorización es:
( x + 3/5)² = 49/25
Se extrae la raíz cuadrada en ambos miembros y se despeja la variable x:
x + 3/5 = ± 7/5 , por lo que x=-3/5 ±7/5
Entonces, se llega a la solución:
x = 4/5
x=-2
| Ventajas | Desventajas |
|---|---|
| Caso útil si queremos entender la estructura de una ecuación cuadrática. | Es complejo y no es fácil de comprender para todos. |
| Esencial para derivar la fórmula cuadrática. | Requiere mucho cuidado al trabajar con manipulaciones algebraicas. |
3.- Fórmula general
Es el método más completo y seguro para encontrar la solución de una ecuación cuadrática. Está dada por:
x = [–b ±√(b² – 4ac)]/2a , donde a,b y c son constantes.
Por ejemplo; resolvamos x² – 5x + 6 = 0, utilizando la fórmula cuadrática
Lo primero es comparar la ecuación con la ecuación general de una cuadrática. ax² + bx + c = 0, donde se observa que a = 1 , b = –5 y c = 6
Sustituyendo estos valores en la fórmula cuadrática,
x = [-(-5)±√{(–5)²– 4(1)(6)}]/2(1)
x = [5 ± √{25 - 24}]/2
x = [5 ± √{1}]/2
x = [ 5 ± 1]/2
Separando las dos soluciones,
x = (5 + 1)/2
x=3
x = (5 – 1)/2
x = 2
| Ventajas | Desventajas |
|---|---|
| Es un caso general de uso para todas las ecuaciones cuadráticas. | Puede llevar más tiempo que otros métodos, especialmente en simplificaciones complejas. |
| Proporciona un método directo y confiable. | Se debe memorizar la fórmula. |
4.- Método Gráfico
Este método se utiliza para resolver ecuaciones cuadráticas de forma gráfica. Para obtener estas soluciones se debe hallar dónde se encuentra el eje x en la gráfica y ubicar el punto que proporciona la solución a la ecuación.
Por ejemplo, para resolver la ecuación x² – 4x + 3 de forma gráfica, lo primero que se debe hacer es hallar las coordenadas del vértice:
x = ( -(b/2a)
x = - (-4/(2.1))
x= 2
y = x² – 4x + 3
y = (2)² - 4(2) + 3
y = -1
Entonces las coordenadas del vértice son: (2 , -1)
Ahora, pqra encontrar el punto o los puntos de corte con el eje X, igualamos la función con 0, y se aplica la fórmula general para ecuaciones de segundo grado:
x² – 4x + 3 = 0
x = [–b ±√(b² – 4ac)]/2a
x = 4 ± √(16 – 12)]/2
x = (4 ± 2) / 2
x= (4 + 2) / 2
x = 3
x= (4 - 2) / 2
x = 1
Entonces se han encontrado dos puntos de corte los cuales son: (3 , 0 ) y (1 , 0)
Ahora, para halalr el punto de corte con el eje Y, basta con conocer el valor de la constante, que en este caso es 3, por tanto las coordenadas son: (0 , 3)
Una vez se tiene todas estas coordenadas, se procedo a graficar:
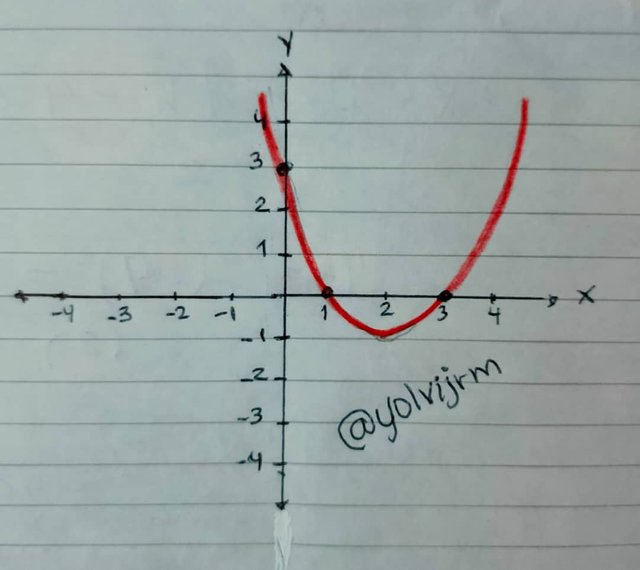
| Ventajas | Desventajas |
|---|---|
| Proporciona una representación visual de las soluciones. | Depende únicamente de mecanismos y técnicas de gráficos precisos. |
| Esencial para comprender el comportamiento de una función cuadrática. | Puede que no proporcione la solución exacta en los casos en que las intersecciones con el eje x sean números enteros. |
Resolver la ecuación lineal 3x + 2 = 11 y mostrar el valor de x.
Para hallar la solución de esta ecuación se siguen los siguientes pasos:
| Ecuación | 3x + 2 = 11 |
|---|---|
| Agrupar los términos independientes en un solo miembro | 3x = 11 - 2 |
| Realizar las operaciones algebraicas | 3x = 9 |
| El 3 que acompaña la x pasa al otro miembro | x = 9/3 |
| Entonces | x = 3 |
A contiuación se muestran los cálculos que se han realizado para ello:

Resuelve esta ecuación cuadrática x² + 2x - 6 = 0.
Para hallar la solución de esta ecuación se empeló la fórmula general para ecuaciones de segundo grado:
| Ecuación | x² + 2x - 6 = 0 |
|---|---|
| Aplicar la fórmula general | x = [–b ±√(b² – 4ac)]/2a |
| Se sustituyen los valores | x = [–2 ±√(2² – 4(1)(-6)]/2(1) |
| Realizar las operaciones correspondientes | x = [–2 ±√(28)]/2 |
| Se obtienen los cuadrados perfectos | x = [–2 ±(√4)(√7)]/2 |
| Se determinan las raíces | x = [–2 ± 2(√7)]/2 |
| Dividiendo entre 2 | x = –1 ± √7 |
| Entonces | x = –1 + √7 y x = –1 - √7 |
A contiuación se muestran los cálculos que se han realizado para ello:

Escenario número 1
Supongamos que Ali tiene 15 dólares para gastar en snacks. Compra un paquete de patatas fritas por 3 dólares. ¿Cuánto dinero le queda?
Supongamos que x es la cantidad de dinero que le queda a Ali.
Ecuación: x + 3 = 15
Comparte una solución para x
Se tiene que x es la cantidad de dinero que le queda a Ali, entonces la ecuación está dada por x + 3 = 15
| Ecuación | x +3 = 15 |
|---|---|
| Se agrupan los términos independientes en el mismo miembro | x = 15 - 3 |
| Se realiza las operaciones algebraicas | x = 12 |
Entonces, se tiene que a Ali le quedan $12 después de gastar $3 de un total de $15.
Escenario número 2
Supongamos que hay una pelota que se lanza en dirección ascendente desde el suelo con una velocidad inicial de 20 m/s y la altura de la pelota sobre el suelo se presenta mediante la siguiente ecuación:
h(t) = -5t² + 20t
Aquí h es la altura en metros y t es el tiempo en segundos.
¡Comparte sobre la altura máxima alcanzada por esta pelota!
Se tiene que la ecuación h(t) = –5t² + 20t representa la altura de la pelota sobre el suelo en función del tiempo t. La altura máxima de la pelota se alcanza cuando la velocidad vertical es cero
Para determinar la altura máxima, se necesita saber el tiempo en el que la pelota alcanza el punto más alto. Esto ocurre cuando la velocidad es igual a 0.
Entonces, para obtener la función velocidad, vamos a encontrar la derivada de la altura h.
V(t) = dh/dt = d/dt(–5t² + 20t)
V(t) = –10t + 20
A la altura máxima, la velocidad es 0.
Por lo tanto.
| Ecuación | 0 = –10t + 20 |
|---|---|
| Se agrupan los términos independientes | -10t = –20 |
| El 10 que acompaña la incógnita de pasa al otro miembro | t = -20/-10 |
| Entonces | t = 2 |
Con el valor de t obtenido lo sustituimos en la ecuación de la función altura.
| Ecuación | h(t) = –5t² + 20t |
|---|---|
| Se sustituye el valor de t | h = –5(2)² + 20(2) |
| Se realizan las operaciones algebraicas correspondientes | h = – 20 + 40 |
| Entonces | h = 20 |
La altura máxima (h) alcanzada por la pelota es de 20 metros.

Gustoso de presentar mi participación en este concurso; aprovecho la oportunidad de invitar a @petrarodriguez, @damisvilladiego y @sabrip a que participen en esta actividad:
SLC S22W4//Linear and Quadratic equations
Las imágenes son de mi propiedad, tomadas con Infinix Note 40 Pro.
Cc: @khursheedanwar
¡Saludos y bendiciones!

Congratulations, your post has been upvoted by @scilwa, which is a curating account for @R2cornell's Discord Community. We can also be found on our hive community & peakd as well as on my Discord Server
Felicitaciones, su publication ha sido votado por @scilwa. También puedo ser encontrado en nuestra comunidad de colmena y Peakd así como en mi servidor de discordia