"SLC-S22W4//Linear and Quadratic equations equations."
Invito a participar en el concurso "SLC S22W4//Linear and Quadratic equations" a los amigos @chefdanie @akmalshakir y @mohammadfaisal.

Las ecuaciones ideales se trata igualdades que involucran variables o incógnitas cuyo valor es desconocido y está referido a un único valor, en las ecuaciones lineales la mayor potencia de las incógnitas es igual a 1, para solucionar una ecuación es necesario aplicar algunas operaciones para encontrar el valor de las incógnitas o variables que la conviertan en una identidad, al representar la ecuación en un sistema cartesiano de coordenadas su gráfica resulta ser una línea recta.
Su forma general viene dada por
X - 3 = 2
Las ecuaciones cuadrática se define como una igualdad donde el mayor exponente o exponente de la variable es igual a dos, existen varios métodos para determinar los valores de las variables entre los que destacan la factorización, completación de cuadrados, mediante la aplicación de la fórmula cuadrática y el método gráfico, la ecuación cuadrática se diferencia de la lineal porque al ser representada en un sistema cartesiano de coordenadas quedará representada por una parábola.
Su forma general es:
x2 + 3x - 6 = 0
Para obtener los valores de las incógnitas de una ecuación cuadrática existen algunos métodos que estaremos explicando a continuación Resolviendo algunos casos puntuales.
Factorización
Este método es ampliamente utilizado para determinar los valores de raíces de la ecuación, en forma resumida y rápida, cosiste en transformar un trinomio en binomios de menor grado, este método es aplicable sólo para ecuaciones que se puedan factorizar.
Ejemplo de aplicación:
x2 + 2X - 8 = 0
Buscando dos números que sea múltiplo 2y que al multiplicarlo entre sea igual al el valor del término independiente.
(X+4)(X-2) = 0
Luego estos binomios se iguala a "0" para obtener los valores de la variable "x".
(X+4) =0
X = -4
Luego
X - 2 = 0
X = 2
Con lo que se demuestra que se determina que la solución es;
{X1 = -4 y X2 = 2 }
Método de completación de cuadrados
Este método es más extenso y exigente en cuanto a operaciones de cálculo se refiere, consiste en transformar la ecuación en un trinomio perfecto.
Ejemplo: si se tiene la siguiente ecuación dada en la tarea (3), obtener los valores de "x".
X2 + 2X - 6 = 0
a = 1 ; b = 2 ; c = -6
El requisito principal para utilizar este método es que el coeficiente a = 1, lo cual se cumple para este caso, si "a" es diferente de 1, se debe transformar la ecuación dividiendo por el valor de "a".
Luego se toma el coeficiente "b" y se divide entre 2 y se eleva a la segunda potencia.
(b/2)2
Seguidamente sumamos y restamos este valor en la ecuación para producir alteraciones en la misma quedando de la forma:
(b/2)2= 2/2 = 1
(X + 1 )2 - 1 - 6 = 0
Entonces Aislando el binomio, se tiene:
(X + 1 )2 = 7
Para eliminar el cuadrado, metemos en raíz cuadrada ambos lados de la ecuación:
√(X + 1 )2 = √(7)
Simplificando queda:
X + 1 = √(7)
Entonces, las 2 raíces de la ecuación se calculan así:
X1 + 1 = √(7)
X1 = √(7) - 1
X2 + 1 = - √(7)
X2 = -1 - √(7)
Con lo que queda demostrado que resultado de la ecuación dada en la tarea (3) utilizando el método de completación de cuadrados es:
{ X1 = √(7) - 1 ; X2 = -1 - √(7) }
Método de la fórmula cuadrática
Para ilustrar este método de cálculo de las raíces de la ecuación, estaremos utilizando nuevamente el ejercicio dado en la tarea (3) de esta clase.
X2 + 2X - 6 = 0
Donde
a= 1 ; b = 2 ; c = -6
Aplicando la fórmula para calcular las raíces se tiene que:
X= -b ±/‐ √(b2 - 4(a)(c)) / 2 (a)
Sustituyendo valores queda:
X= -2 ± √(22 - 4(1)(-6)) / 2 (1)
Sacando factor común
X= -2 ± √4 √((1+6) / 2
X = -2 ± 2 √7 /2
Simplificando se tiene:
X = -1 ± √7
Entonces las raíces de la solución son:
X1 = -1 + √7
X1 = √7 - 1
X2 = -1 - √7
Con lo que se demuestra la solución de la tarea (3)
{X1 = √7 - 1 ; X2 = -1 - √7}
Método Gráfico
Este método permite obtener una solución de las raíces de la ecuación cuadrática, mediante la representación en el sistema cartesiano de coordenadas, para lo cual se obtienen los puntos de corte de la parábola con el eje de coordenadas "x".
X2</sup/> + 2X - 6 = 0
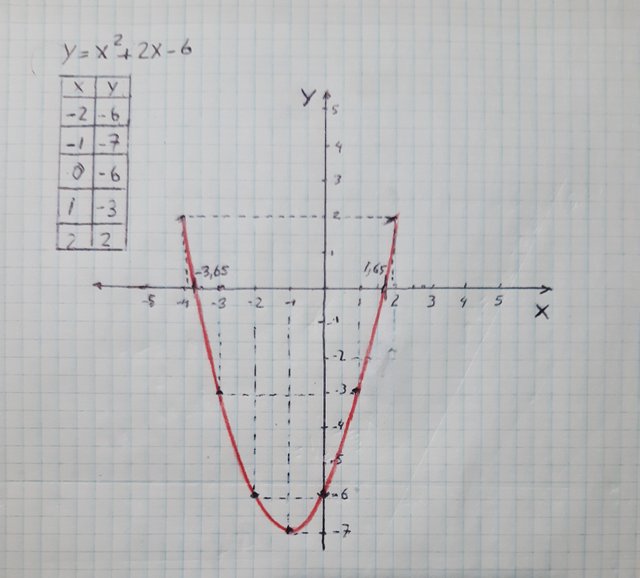
Partiendo de que se calcularon las raíces de la ecuación cuadrática, se tiene: Y = X2 + 2X - 6 = 0 Entonces: (X - (√7 - 1)) (X -+ (1 + √7)) = 0 Los puntos de corte con el eje "x" son: (X - (√7 - 1)) = 0 X = (√7 - 1) = 2,65 - 1 = 1,65 (X + (1 + √7)) = 0 X = - (1 + √7)) = - (2,65+1) = -3,65 Teniendo los valores donde la curva intercepta al eje "x" que son x=1,65 y x=-3,65 ; procedemos a generar otros ((x,y,) para realizar la gráfica de la ecuación. Gráficando valores la curva de la ecuación queda de la siguiente manera:
X Y -4 2 -3,65 0 -3 -3 -2 -6 -1 -7 0 -6 1 -3 1,65 0 2 2
| Método decálculo | Ventaja | Desventajas |
|---|---|---|
| Factorización | - Operaciones de cálculo rápidas y sencillas, facilitando la obtención de las raíces de la ecuación cuadrática. | Aplicación reducida porque no todas las ecuaciones son factorizables. |
| Completación de cuadrados | Método Aplicable a cualquier tipo de ecuación cuadrática | Incorpora operaciones de más complicadas al proceso de cálculo, lo que dificulta la obtención de lasraíces de la ecuación y hay que tener cuidado de no cometer errores al realizar las operaciones. |
| Fórmula cuadrática | Este método simplifica la obtención de las raíces de la ecuación. | Este método hay que trabajarlo con mucho cuidado de no cometer errores, ya que Incorpora una raíz al proceso de cálculo y a muchas personas le desagrada trabajar con estos elementos. |
| Método gráfico | Método sencillo de fácil desarrollo, aplicable a todas las ecuestiones cuadráticas, permite ilustrar de forma gráfica la curva de la ecuación que se está trabajando, lo que facilita su comprensión. | Este método es el más trabajoso, ya que además del proceso de cálculo hay que representar la gráfica dela ecuación en el sistema cartesiano de coordenadas, no es preciso cuando se trabaja de forma manual. |
Resolver la ecuación lineal 3x + 2 = 11 y mostrar el valor de x.
Este ejercicio será resuelto mediante la aplicación operaciones que permite aislar y determinar el valor de la variable o incógnitas, para ello iniciaremos restando (-2) en ambos lados de la ecuación, luego procedentes a multiplicar ambos lados de la ecuación por (1/3), con lo que queda despejado el valor de la variable "x".

• Resuelve esta ecuación cuadrática x^2 + 2x - 6 = 0.
Esta ecuación se resolverá aplicando la fórmula cuadrática, que permitirá obtener los valores de las variables o raíces de la ecuación.

Luego de aplicar la fórmula cuadrática y ejecutar las operaciones que la misma involucra, finalmente se obtiene que los valores de las raíces son:
{X1 = √7 - 1 ; X2 = -1 - √7}
Supongamos que Ali tiene 15 dólares para gastar en snacks. Compra un paquete de patatas fritas por 3 dólares. ¿Cuánto dinero le queda?
Supongamos que x es la cantidad de dinero que le queda a Ali.
Ecuación: x + 3 = 15
Comparte una solución para x
El ejercicio se resolverá mediante la aplicación de operaciones álgebraicas de resta sencilla, lo que permite obtener el valor de la variable.

Con el resultado obtenido, se puede concluir que a A Ali le quedan 12$ para gastar en snacks.
Supongamos que hay una pelota que se lanza en dirección ascendente desde el suelo con una velocidad inicial de 20 m/s y la altura de la pelota sobre el suelo se presenta mediante la siguiente ecuación:
h(t) = -5t^2 + 20t
Aquí h es la altura en metros y t es el tiempo en segundos.
¡Comparte sobre la altura máxima alcanzada por esta pelota!
Por favor resuelva para h!
En este ejercicio de lanzamiento vertical, se de la ecuación cuadrática que define el desplazamiento de la pelota en función de la variable tiempo, con la cual se determinará la altura máxima que la misma alcanza, pero antes de ello, la utilizaremos para determinar el tiempo tiempo empleado por la misma para alcanzar la altura máxima, teniendo en cuenta que la variación del desplazamiento en el tiempo es igual a la velocidad, es decir decir que dh(t)/dt = V(t), además se conoce que en un lanzamiento vertical cuando el móvil, en este caso la pelota, alcanza la altura máxima su velocidad es 0 m/s, por lo que con ese dato procedemos a determinar el tiempo máximo como se indica a continuación:

Una vez que se tiene el tiempo que emplea la pelota en alcanzar la altura máxima, ese valor de tiempo obtenido se sustituye en la ecuación que define el desplazamiento de la pelota en función del tiempo, lo que nos permite determinar la altura máxima alcanzada por la pelota, cuando ésta es lanzada con una velocidad inicial de 20 m/s desde el suelo.

Con el resultado obtenido, podemos afirmar que la altura máxima alcanzada por la pelota es:
Hmax= 20m.
Sin más que agregar queridos steemians, me despido, espero les haya gustado la publicación, hasta la próxima oportunidad.
Las fotografías son de mi propiedad, tomadas con un teléfono Samsung Galaxy A30.
Para saber más de mí, aquí dejo mi Logro1.
Congratulations, your post was upvoted by @supportive.
https://x.com/Saulvama0/status/1878476638905651583?t=0XaLCVAkc-t6Ao2iSZ0gzw&s=19
@tipu curate 2
Upvoted 👌 (Mana: 1/7) Get profit votes with @tipU :)
Congratulations, your post has been curated by @dsc-r2cornell. You can use the tag #R2cornell. Also, find us on Discord
Felicitaciones, su publicación ha sido votada por @ dsc-r2cornell. Puedes usar el tag #R2cornell. También, nos puedes encontrar en Discord