SLC S22W4||Linear and quadratic equations

Source

Linear and quadratic equations

Linear and quadratic equations are most significant concepts in field of algebra so they have differences in form of their degree,their general form as well as in their graphical representation and many more so let's have a look at them one by one.

Linear equations

Linear equations are those which are having a degree of 1 so it means that their highest power is 1 in case of variable which is x mostly.General form of linear equation can be written as follows;

ax + by = c

In the above linear equation a, b and c are constants but x and y can change that's why these are variables....

2x + 3y = 5

Above is an algebric example in which x and y are variables as they can alter and 2, 3 and 5 are not changeable so these are constants.Linear equations may be represented as straight lines at coordinate plane in their graphical presentation.

Practical example of linear equation can be taken as follows;

Suppose there is a car rented so it's 40$ cost is fixed so 40$(Fixed cost)+$20(for each hour).If you have to write equation for car rented for x hours then total cost may be represented by linear equation as 20x+40.

Graphical presentation

Quadratic equations

Quadratic equations re those having degree of 2 so it means 2 will be highest variable power in this case.General form of quadratic equation may be written as follows;

ax^2 + bx + c = 0

Here a, b and c are constants and again x is a variable present in this quadratic equation.

Algebric example can be written as;

x^2 + 4x - 3 = 0

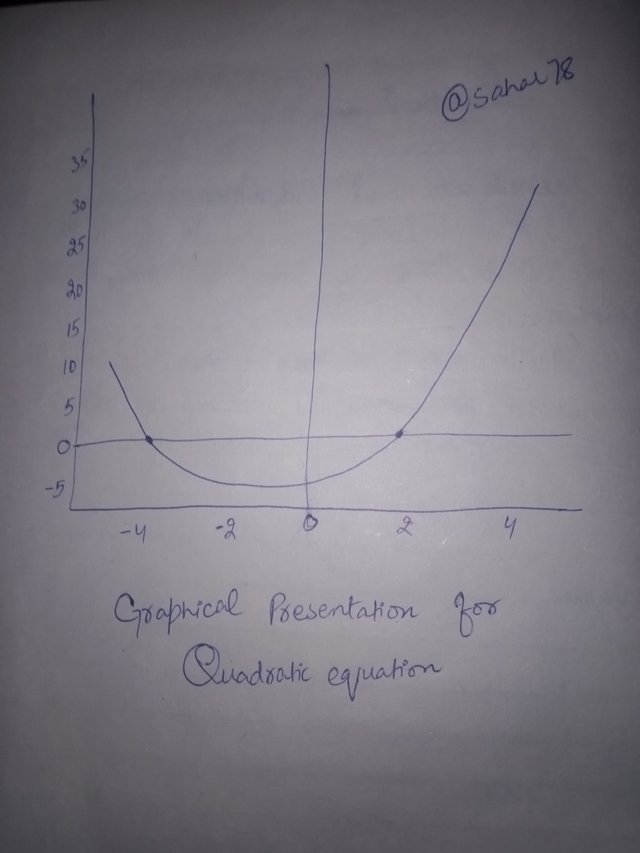
Here x can vary so it's a variable and 1, 4 and -3 are not able to change so these are constants.These may be represented at coordinate plane in form of parabolas.

Practical example may be written as;

Suppose a ball has been thrown in upward direction from ground and height of ball after x second is h=-4x^2+20x+0 so suppose that 4x^2 is resistance of air.

Graphical presentation

Difference	Linear equation	Quadratic equation
Degree	1	2
General form	ax+by=c	ax^2+bx+c=0
Graph	Straight line	Parabola
Solution	One solution	Two solution

Methods for solving quadratic equations

Method 1: Factoring

Factoring is defined as expression of quadratic equation as product of two binomials together and then providing a solution for variable.

x^2 + 5x + 6 = 0 may be factorized as (x + 3)(x + 2) = 0.

Pros	Cons
Precise,Simpler, straightforward	Restricted in solutions and limited to quadratic equation
Quadratic equation may be solved out with integer root	Don't suitable for equations which are with irrational roots

Method 2: Quadratic formula

Quadratic formula is another significant method used for solving quadratic equations of form ax^2 + bx + c = 0.

Below is a formula used for solving quadratic equation;

x = (-b ± √(b^2 - 4ac)) / 2a

x^2 + 4x - 3 = 0 may be solved by use of quadratic formula.

Pros	Cons
May be used for solving any kind of quadratic equation	May be complicated in its implementation
Provide precise solutions for irrational roots	Included those algorithms which are complicated.

It's step by step solution is in picture shared below:

Method 3: Graphing

Graphing is another important method to plot quadratic equation at coordinate plane and to find out x-intercepts.

x^2 + 4x - 3 = 0 may be graphed for finding out x-intercepts.

Pros	Cons
Helpful in solutions identification with visual presentation	Exact solutions can't be extracted
Used for solutions estimation	Restricted to quadratic equations as these are easy for graphing.

It's step by step solution is in picture shared below:

Solution based task

Part 1 for solving linear equation

Part 2 for solving quadratic equation

Graphical presentation

Scenerio based task

Part 1 for getting value of x

Part 2 for getting value of h