SLC-S22W4//Linear and Quadratic equations equations.

Linear and Quadratic equations equations
Hello my friends and dear mathematicians. Greetings to you all. I suppose we are doing so well and ready to engage this week with our amazing entries on this amazing topic in week 4 of the steeemit Learning challenge.
In the previous class, we discussed on linear equations and the various methods of reserving them. Simultaneously we made mention of methods Of reserving linear simultaneous equations which are: elimination, substitution, graphical and Matrix method.
We also discussed on how these problems could be a replied in real world problems and resolved equally.
Coming to this week, our work continues on the algebra, but then this time we'll be going a little bit deeper which we are going to discuss on other forms of equations In algebra. This week our main focus is linear equation and quadratic equations.
By definition, a linear equation is any equation given in the form where highest power of the leading term in the equation is 1. Linear equations are often comprised of binomials. A quadratic equation is simply an inclination of the power in a linear equation and adding one more term to it.
Elaborate on the difference between linear and quadratic equations. Give examples of each type of system of equation and describe their general forms as well.
Linear equation
Definition:
A linear equation is any given equation representing a straight line graph. This equation has its highest power or degree of the binomial as 1 on each variable.
Linear equations generally exist in two form.
- One variable.
This is a linear equation in which they are just two terms, With one variable. The highest power of the variable is 1.
For instance ax +b = 0
Example 3x – 2 = 0
- Two variable.
Linear equations can also exist in two variable. Meaning there exists two terms with two separate Distinct variables. The highest power of each variable is still 1.
This can be equation in the forms ax + by = c
Example:
2x + 3 = 7
Quadratic Equation
Definition:
Quadratic equations are a family of equations representing parabolas graphically. These equation usually take a u-shape on a curve or n-shape And it can be located on any of the four quadrant of the Cartesian.
The highest degree of a quadratic Equation is 2 And they are represented in descending on order of preceding terms.
The general form representation equation is given by:
mx² + nx + p = 0
Example:
x² – 5x + 6 = 0
2x² – 3x – 2 = 0
Key differences
| Features | Linear equation | Quadratic Equation |
|---|---|---|
| Degree | 1 | 2 |
| Graph | straight line | parabola |
| Solution | one solution | Two solution |
A system of linear equations can be resolved as pair. Such as the case of linear simultaneous equations.
This can be resolved using any of the methods of solving linear equations.
Example.
3x + 2y = 7
4x – y = 3
Quadratic system may involve a linear and a quadratic. This can be resolved by combining solutions of the 2 equation. That is making one the subject of the formula and applying it in the other equation. This easy equation in most case is to substitute the linear equation in the quadratic.
Example.
y = x² – 4
y = 2x – 1
Describe the various methods for solving quadratic equations and share pros and cons for each method.
To begin with, there are four basic methods of solving Quadratic Equation namely
- Factorization
- Completion the square
- formula method and
- Graphical method.
1) Factorization
Solving Quadratic Equation by factorizing is a method which embodies looking for the zeros of the equation and then applying the zero product law for find the solutions.
Zero product law.
If A and B are to factors of a quadratic, then
A×B = 0
Therefore
A = 0 or B = 0
Example.
Factorize the following quadratic equation.
x² – x – 6 = 0
Solution.
We are going to use the notion if a general quadratic equation,
ax² + bx + c = 0
To factorize : Look for the factors of the product ac which;
- When add will give
b - Multiply back gives
ac
ac product is –6, now factors of –6(±1, ±2 ,±3, ±6)
To have – 1 the factors required are (2, –3)
The equation becomes
x² + 2x – 3x – 6 = 0
factorize by grouping
(x² + 2x) – (3x – 6 )= 0
x(x + 2)– 3(x + 2) = 0
(x + 2)(x – 3) = 0
applying zero product law.
(x + 2) = 0 »» x = –2
Or
(x – 3) = 0 »» x = 3
| Pros | cons |
|---|---|
| Quick and fast way of Resolving simple quadratic equation | Not always applicable, some quadratic equations cannot be factorized |
| Provide a strong basis for understanding other algebraic concepts | It could be complex in cases of complex quadratics. |
2) completing the square.
This is a crucial method of solving quadratic equations. Can need to be taken and this should be done appropriately in order to arrive at the final solution. A few steps are required to complete a square when resolving equations.
Make the coefficient of x² unity.
½ the coefficient of x, Square the term and add to either sides of the quadratic equation.
This will make the left hand side a perfect square.
Take the square root(√) of both sides of the equation to away the Square.
Simplify terms to get the values of x.
Example.
Solved the following Quadratic equation by completing the square. 2x² – 3x – 2 = 0
Solution.
The coefficient of x must be unity, that is one so we proceed by dividing all through by 2
x² – 3/2x – 1 = 0
Half the question of x, square it and add to both side of the equation
x² – 3/2 x + (½(–3/2)² = 1 + (½(–3/2)²
This will make the right hand side a perfect square
(x – 3/4)² = 1 + 9/16
Finding the LCM of the right hand side
(x – 3/4)² = 25/16
Taking the square root of both sides.
√(x – 3/4)² = ± √(25/16)
(x – 3/4) = ± 5/4
Open the brackets and simplify.
x = 3/4 ± 5/4
Separating the solutions,
x = 3/4 + 5/4 »»» x = 8/4 ,
x = 2
Or
x = 3/4 – 5/4 »»» x = – 2/4
x = –½
Note: for Any quadratic, taking the square root of both sides, we must add ± In front of the square root sign (±√) Since there exist two solutions.
| Pros | Cons |
|---|---|
| Useful case if We want to understand the structure of a quadratic equation | It is complex and not easily grasp By everyone. |
| Essential in deriving the Quadratic formula | requires much care when working with I algebraic manipulations |
3) Formula method.
This is carried on by use of the quality formula. Usually given by.
x = [–b ±√(b² – 4ac)]/2a
Where a,b and c are constants.
Example.
Solve the following equation using quadratic formula
2x² – 3x – 2 = 0
Solution.
We start by comparing the equation with The general equation of a quadratic. ax² + bx + c = 0
Observing, we see that a = 2 b = –3 and c = –2
Substituting these values in the quadratic formula,
x = [––3±√{(–3)²– 4(2)(–2)}]/2(2)
x = [3 ± √{9 +16}]/4
x = [ 3 ± √{25}]/4
x = [ 3 ± 5]/4
Separating the two solutions,
x = (3 +5)/4 = 8/4
x = 2or
x = (3 – 5)/4
= – 2/4
x = –½
| Pros | Cons |
|---|---|
| Is a general case use for all quadratic equations | It can be more time consuming than other methods, especially in complex simplifications. |
| It gives a direct and a reliable method | students need to memorize the Formula. |
4) Graphical method
This method is used to resolve battery equations. Graphically. To obtain these solutions, We need to look for where the graph gets the x-axis and locates the point which gives our solution to the equation.
Example.
Solve The following quadratic equation. Graphically
x² – x – 6 = y
Solution:
- Intercepts
Obtained by setting the values of X and y to be equal to zero on their various intercepts.
x² – x – 6 = y
At x–intercept, y = 0
Therefore x² – x – 6 = 0
Solving the equation by factorizing.
(x + 2)(x –3) = 0
»» x = –2 or x = 3
👉 Points (-2, 0 ) & (3, 0)
At the y–intercept, x = 0
»» y = 0² – 0 – 6
y = –6
👉 Points (0, –6)
- Minimum value
This is given the the formula [4ac – b²]/4a
From the equation a = 1 b = –1 & c = –6
In the formula
[4(1)(–6) – (–1)²]/4(1)
= [– 24 – 1]/4
= – 25/4
»» min value = – 25/4
- Line of symmetry (it divide the curve into 2)
x = –b/2a
»» x = ––1/2(1)
x = ½
- Turning point.
The coordinates of the turning point consists of minimum value and the line of symmetry.
T P (½ , –25/4)
Graph
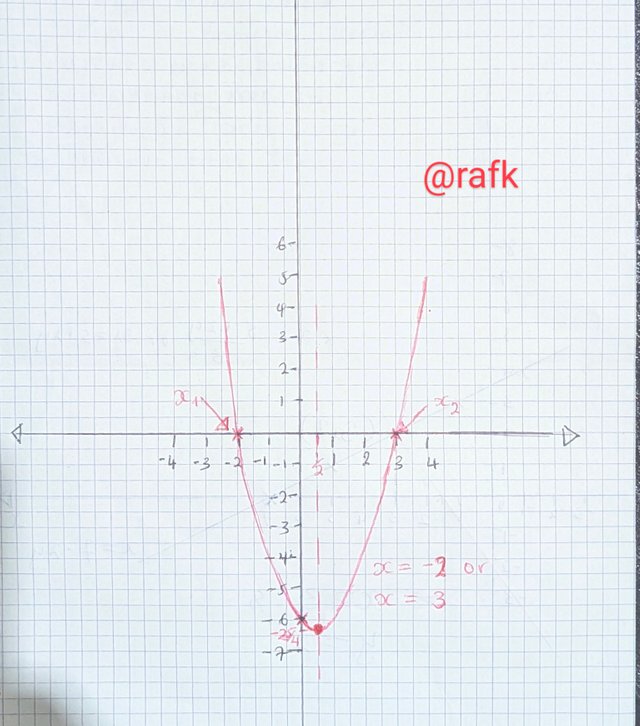
Note: The turning points are determined by the values of a, The coefficient in x². If the value of a is positive, then there will be a minimum turning Point. Otherwise negative. It is a maximum turning Point.
| Pros | Cons |
|---|---|
| It gives a visual representation of solutions | depends solely on accurate graphing mechanisms and techniques |
| Essential for understanding the behavior of a quadratic function. | May not provide the exact solution In cases where the x-intercepts are integers. |
Consideration:
One equation have been used repeated In more than one method To prove that what ever method we are using gives us the same solution.
Solving linear and quadratic equation

Above is a clear illustration of the two solutions which are
- Linear equation
- Quadratic equation.
Note: We are not limited to the formula method as other methods such as completing the square and graphical methods could also be applied in the second part of the question.
However, there exist no factors the second equation which is quadratic, therefore, there is the need to employ other methods of solving quadratic equations. This is one of the disadvantages of using factorization method when dealing with not all problems have factors or zeros.
Task 4

Here is a detail step-by-step approach in order to resolve the above raised question.
Steps to follow.
problem statement
- Ali have $15 to spend on snacks
- Ali buys a pack of chip cost $3
- Find how how much money he left with afterwards.
Equation
If x is the amount of money Ali has left, then the equation is given by x + 3 = 15
Solution
x +3 = 15 {We subtract 3 from both side of the equation}
x +3 – 3 = 15 – 3
x = 12
Results
Therefore, Ali is left with $12 after spending $3 out of $15 total.
Affirmative
The solution is accurate, hence mathematically correct which strengthen its application in resolving real world problems.
Limitations
This method is strictly applicable to resolving linear equations in one variable. However, it would not be applicable in a system of linear equations or other forms of equations.

This is an application of qualification in real world problems. Let's see the theater approach on how this can be resolved.
Assumptions
- The ball is thrown vertically upward.
- there is no other resistance acting on the ball
- provided the acceleration due to gravity remains constant with a value of 9.8ms-²
Problem statement
- The equation h(t) = –5t² + 20t represent the height of the ball above the ground as the function of time t.
- The maximum height of the ball is attained when the vertical velocity is zero.
Solution
To determine the maximum height, we need to know the time when the bar reaches the highest point. This occurs when the velocity is equal to 0.
- velocity function.
To obtain the velocity function, we are going to find the derivative of the height h.
V(t) = dh/dt = d/dt(–5t² + 20t)
V(t) = –10t + 20
At maximum height, the velocity is 0.
Therefore.
0 = –10t + 20
Minus 20 from either sides of the equation. .
-10t + 20 – 20 = 0 – 20
–10t = –20
Divide from both sides by -10.
-10t/-10 = -20/-10
»»» t = 2 seconds
With the value of t obtained, we substitute it in the equation of the height function.
h(t) = –5t² + 20t
-----» h(2) = –5(2)² + 20(2)
= – 20 + 40
= 20 meters
Maximum height (h) reached by the ball is 20 m.
Limitations
- Air resistance cannot be completely zero.
- The acceleration due to gravity g varies slightly at some point depending on the location.
Alternative method:**
Applying calculus this problem it's really light work for those who understand the concept and theory better. Considering the fact that we are still on equations, we are going to see how this could work in our context of reserving quadratic equation.
An alternative approach could be by completing the square of this function. Let's see how this works.
I have made mention of the various procedure in completing the square under a section in this lesson. Here we are not going to be more specific but apply the method directly.
h(t) = –5t² + 20t
- Factor out –5 to make t² unity(1)
h(t) = –5(t² – 4t)
- ½ The coefficient of x add and subtract on the same side (applicable method when resolving quadratic functions)
h(t) = –5[t² – 4t +{½(–4)}² – {½(–4)}²]
- simplifying
h(t) = –5[t² + 4t +(–2)² – {–2)}²]
- t² + 4t +(–2)² it's a perfect square (t –2)²
h(t) = –5[(t –2)² – {–2)}²]
- simplify
h(t) = –5[(t –2)² – 4 ]
- multiply by –5
h(t) = –5(t –2)² + 20
By rules of resolving quadratic functions, 20 represents the maximum height of the ball, which is 20 m. And this occurs when
t –2 = 0 or
t = 2 (line of symmetry)
Therefore t = 2 seconds
This can be represented together as the coordinates of the maximum turning point as (2, 20). Which we have mention of earlier.
Results:
Assuming negligible and resistance, the ball takes 2 seconds to reach the maximum height which is 20 m.
| Conclusion |
|---|
Working with algebra is a better way to strengthen our knowledge in mathematics. However, it is necessary to begin from the basics and get some more complex cases as we proceed ahead. Linear and quadratic equations be more applicable and informative in modeling with real life problems When applied in such conditions.
So in on a good note, I will invite the following three persons to join me with their distinctive knowledge on this topic.
Cc: @khursheedanwar
Best regards: @rafk