SLC-S22W4//Linear and Quadratic equations equations.

_{Photo taken from Pixabay}

Hello everyone. Today I will take part in week 4 of Steem Learning Challenge, by @khursheedanwar. This week is focused on linear and quadratic equations, you can find the original post here.

Now, let's get started.

Explain difference between linear and non linear systems of equations. Provide examples of each type of system of equation and describe their general forms.

Before we can talk about the differences between the 2 types, we need to talk about each one of them individually.

Linear Equation

• A linear equation is a equation of the first degree, where the variable can only be raised to the power of1 and are graphically represented by a straight line.
• The general form is: ax + b = 0; where a and b are constants and a cannot be equal to 0
• As an example, we can take: 2x + 3 = 0. And solve it like this:

2x + 3 = 0
Subtract 3 from both sides:
2x + 3 - 3 = 0 - 3
2x = -3
Divide by 2:
x = -(3/2)

• Practical example: An Airport rents cars for a initial fee of $60 + $15 per hour. The total cost of renting a car can be written as:

15h + 60 = Total Cost ; where h is the number of hours

Let's say that I pay a total of $120 . How many hours was the car rented for?

15h + 60 = 120
15h + 60 - 60 = 120 - 60
15h = 60
h = 60/15
h = 4
Answer: I rented the car for 4 hours

And the graph looks like this for the mentioned example:

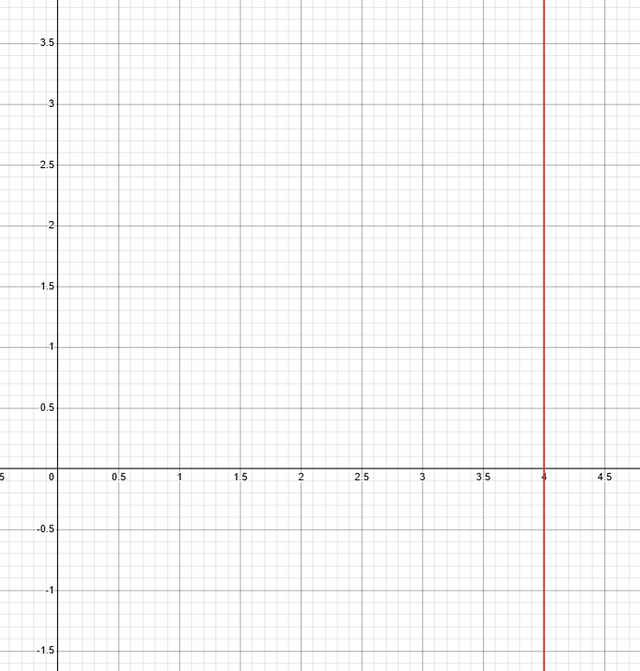
_{Calculator used: https://www.desmos.com/}

Quadratic Equation

• A quadratic equation is an equation of the 2nd degree, as the variable can be raised to the power of 2 and is graphically represented by a parabola
• The general form is: ax² + bx + c = 0; where a, b and c are constants and a cannot be equal to 0
• As an example, we can take: x² - 5x + 6 = 0. And solve it like this:

x^2 -5x + 6 = 0
We can see that this equation can be factored like this:
(x - 2)(x - 3) = 0
From here, we can extract and solve 2 linear equations:
x - 2 = 0
x = 2
and
x - 3 = 0
x = 3

The graph representation can be found below:

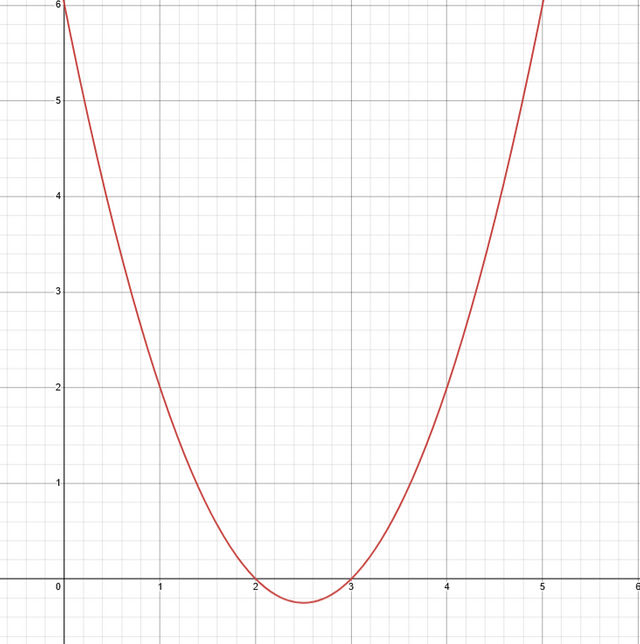
_{Calculator used: https://www.desmos.com/}

• Practical example: I am designing a rectangular yard and have a fixed perimeter of 40 meters. The width is x meters and the length is (20 - x) meters. The area can be written like this: A = x(20 - x) and by doing the multiplications we have: A = 20x - x^2 or A = -2^2 + 20x; where a = -1 and b = 20 and it represents a downward parabola. The maximum area happens at the vertex and we can use the formula:

x = -(b/2a)

In our case, this can be written as:

x = -(20/2(-1))
x = 20/2
x = 10

Now I substitute x = 10 in the area equation to find the maximum area:

A = -10^2 + 20(10)
A = -100 + 200
A = 100

The maximum area is 100 square meters.

Now that we went trough both types of equations, we can write the differences between them:

Type	Linear Equation	Quadratic Equation
Highest power	1	2
General form	ax + b = 0; where a, b are constants and a different than 0	ax^2 + bx + c = 0; where a, b, c are constants and a different than 0
Graph Representation	straight line	parabola
Number of solutions	one	one, two or none

Describe methods for solving quadratic equations and share pros and cons for each method.

In the world of algebra, there are several ways to solve a quadratic equation, each one with it's pros and cons. Usually, we choose the one that we are most comfortable with. Now, let's present some methods.

1. Factoring

• This method implies that a quadratic equation can be written as a product of 2 linear equations.
  Let's take an example:

x^2 - 7x + 10 = 0

To apply the factoring method to this equation, we first need to find the 2 numbers that when multiplying gives us 10 and the sum of them is -7.
We can clearly see that the numbers in question are -5 and -2.
Now, we can factorize the initial equation like this:

(x-5)(x-2) = 0
And solving for x we get:
x - 5 = 0
x = 5
x - 2 = 0
x = 2

And the solution is: x1 = 5 ; x2 = 2

So, we can say that the steps needed to solve a quadratic equation using the factoring method are:

• Step 1: factorize into 2 binomials
• Step 2: solve for x by equaling both of them to 0
• Step 3: Write the solution

The pros of this method:

• It's simple and quick when factors are easy to identify
• Offers good understanding of the roots

Now, the cons:

• It's not effective when the factors are not integers
• Not effective if (b^2 - 4ac) is not a perfect square
• Can be time consuming when we have complex cases

2. Completing the square

• This method is about rewriting the original equation in the form of ax^2 + bx = -c
  Now we can apply these steps:
• Divide by a if a is different than 1
• Add (b/2a)^2 to both sides
• Rewrite the equation as (x + p)^2 = q
• Solve for x by using square roots

Let's consider this example: x^2 + 4x - 5 = 0. Following the steps mentioned above we can solve it like this:

Move the constant to the right side:
x^2 + 4x = 5

Calculate (b/2a)^2, where b = 4 and a = 1:
(4/2)^2 = 4

So we add 4 to both sides:
x^2 + 4x + 4 = 5 + 4
x^2 + 4x + 4 = 9

Rewrite the equation:
(x + 2)^2 = 9
x + 2 = ±3

Solve for x:
x + 2 = 3 => x = 3 - 2 => x = 1
x + 2 = -3 => x = -3 - 2 => x = -5

Write the solution:
x1 = 1
x2 = -5

The pros of this method:

• works for every equation

Now, the cons:

• The process is longer and take more than factoring

3. Quadratic formula

For this method we need to use the formula x = (-b ± √(b^2 - 4ac)) / 2a and apply these steps:

• Identify a, b, and c from the given equation ax^2 + bx + c = 0
• Substitute the values in the formula
• Solve for x

Example: 3x^2 + 5x - 2 = 0. I will solve it using the steps:

Identify the coefficients:
a = 3; b = 5; c = -2

Use the formula: x = (-b ± √(b^2 - 4ac)) / 2a and substitute the values:
x = (-5 ± √(5^2 - 4(3)(-2))) / 2(3)
x = (-5 ± √(25 + 24)) / 6
x = (-5 ± √(49)) / 6
x = (-5 ± 7) / 6

Solve for x:
x = (-5 + 7) / 6 = 2/6 = 1/3
x = (-5 - 7) / 6 = -12/6 = -2

Solution:
x1 = 1/3
x2 = -2

Pros:

• it works for every quadratic equation
• It is a reliable method

Cons:

• It may involve complex numbers if (b^2 - 4ac) is negative
• Is more time consuming for simple equations than factoring

As a summary, we can take a look in the next table:

Method	Pros	Cons
Factoring	quick and fast when factors can be identified easy	Not effective when b^2 - 4ac is not a perfect square
Completing the square	works for every equation	a long process to find the solution for some equations
Quadratic formula	universal for every equation	can include complex numbers if b^2 - 4ac is negative

Linear Equation

We are given the following linear equation that we need to solve: 3x + 2 = 11.

The first step in solving it is to subtract 2 from both sides:

3x + 2 - 2 = 11 - 2
3x = 9

Next, we can divide both sides by 3, to isolate x and find the solution:

3x/3 = 9/3
x = 3

We see that the solution is: x = 3.
The solve for this equation can be found in the image below:

Quadratic Equation

We are given the following linear equation that we need to solve: x^2 + 2x - 6 = 0. From a first look at it, we can extract the necessary terms we need in the quadratic formula that was provided in the lesson: x = (-b ± √(b^2 - 4ac)) / 2a

a = 1
b = 2
c = -6

Before using the formula, we need to compute (b^2 - 4ac). In our case, this is:

(2)^2 - 4(1)(-6) = 4 - 4(1)(-6) = 4 + 26 = 28
Observation: (-) * (-) = (+)

Now we can substitute it in the formula and get:

x = (-2 ± √28)/2(1)
Obs:  √28 = 2√7
x = (-2 ± 2√7)/2

We can write (2 ± 2√7) as 2(1 ± √7). So, when adding it back in the expression for x we have:

x = -2(1 ± √7)/2
We can simplify it by 2, and get the result
x = -1 ± √7

The final solution for this equation is:

x1 = -1 + √7
x2 = -1 - √7

The solve for this equation can be found in the image below:

We can use a online graph calculator and get the parabola for this equation:

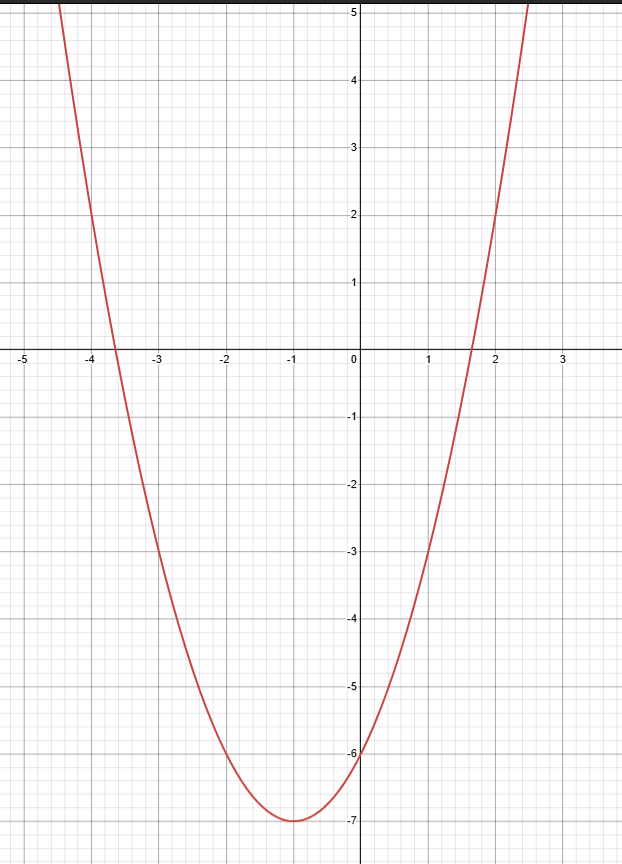
_{Calculator used: https://www.desmos.com/}

Scenario 1

Suppose Ali have $15 for spending at snacks. He is buying a pack of chips for $3. How much money he have left? Suppose x is amount of money Ali has left. Equation: x + 3 = 15

Before we start the solve, we need to identify what type of equation we have. By looking at what was provided to us, x + 3 = 15 we can see that the maximum power of the variable is 1 which means we have a linear equation.

To solve it, we can follow these steps:

• Step 1: apply the subtraction method and substract 3 from both sides:

x + 3  - 3 = 15 - 3
x = 12

• Now, that we found our solution, we can say that after buying the pack of chips, Ali has $12 left to spend.

Scenario 2

Suppose there's a ball which is thrown in upward direction from ground with initial velocity of 20 m/s and height of ball above ground is presented by following equation: h(t) = -5t2 + 20t

For the second scenario, we can see that the biggest power of the variable is 2, which means we are solving a quadratic equation.
To find the maximum height, we can use to parabola vertex formula: -b/(2a) which will also help us find t.
from the original equation: h(t) = -5t² + 20t, we can identify the terms we need:

a = -5
b = 20

Now, we can add them in the vertex formula and obtain:

t = -b/(2a)
t = -20/(2(-5))
t = -20/-10
t = 20/10
t = 2

With t=2, we can go back to the given equation and substitute t:

h(2) =  -5(2)^2 + 20(2)
h(2) = -5(4) + 20(2)
h(2) = -20 + 40
h(2) = 20

We now have our solution h(2) = 20, which means that the maximum height reached by the ball is 20 meters after 2 seconds.

As always, thank you for reading and I'd like to extend an invitation to @ady-was-here, @radudangratian and @cmalescov to take part in this.