SLC-S22W4//Linear and Quadratic equations equations.
| Steemit Learning Challenge -Season 22, Week-4 |
|---|
Task 1
🔰Difference between linear and quadratic equations.
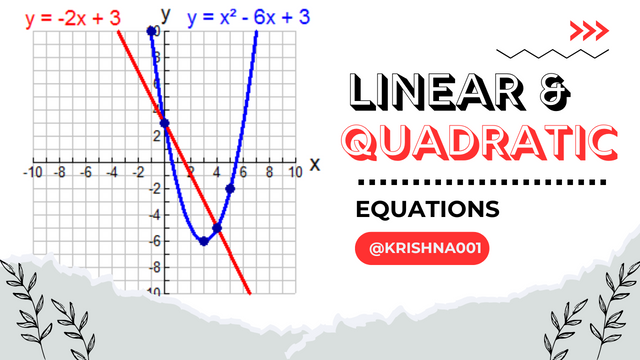
- Linear equations produce a straight line unlike quadratic equations. Quadratic equations produce parabola when their graph is drawn.
- The slope of a quadratic equation keeps changing but that of linear equation doesn't show the same feature.
- Graph of quadratic equation both increases and decreases but that of linear equation either increases or decreases.
- A linear equation is in the form of y = mx+ c while the form of quadratic equation is y = ax2+bx+c.
Task 2
Examples of systems of equations

1- Linear Equation - 3x + 5 = 2y [ General Form- y = mx + c ]
2- Quadratic Equation - 4y = x2+5x+2 [ General Form- y = ax2+bx+c ]
3- Cubic Equation - y = 4x3 [General Form- ax3 + bx2 + cx + d = 0, a ≠ 0]
Methods for solving quadratic equations

There are four methods through which we can solve a quadratic equation which are mentioned below.
1- Factorization method - In this method, we convert the given quadratic expression into the product of two linear factors.
2- Completing the square- This method manipulates the equation to make the left-hand side a perfect square, which leads us to the equation's roots.
3- Quadratic Equation method- In this method, we use a formula which is given below in the picture.
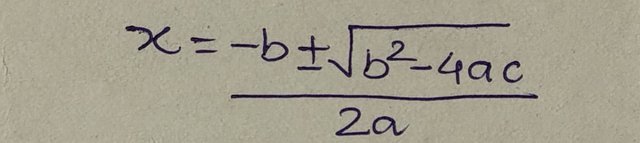
4- Graph method- In this method, we find the intersection points of the two graphs. The x-values of the intersection points are the solutions of our equation.
Pros & Cons of the above mentioned methods: 👇
- Factorization method is easy and fast to find but it is not applicable to all the quadratic equations.
- Completing the square method works always but it is complex and uses multi-steps.
- Quadratic Equation method works for all quadratic equations but it doesn't give any insight.
- Graph method allow us to see the relation of the variables but it is tame taking method.
Task 3
1-Solving for linear equation 3x + 2 = 11 and show value of x.
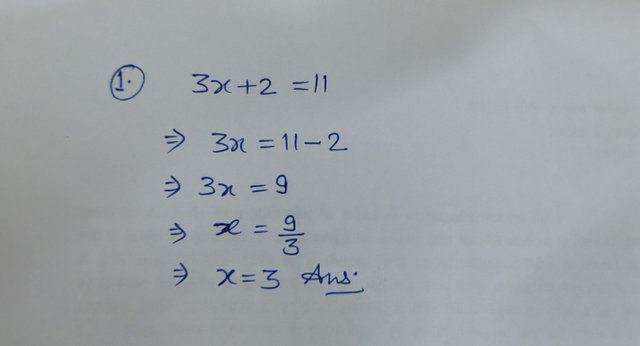
2- Solving for this quadratic equation x^2 + 2x - 6 = 0.

Task 4
Scenario number 1
Suppose Ali have $15 for spending at snacks. He is buying a pack of chips for $3. How much money he have left?

Scenario number 2
Suppose there's a ball which is thrown in upward direction from ground with initial velocity of 20 m/s and height of ball above ground is presented by following equation;
h(t) = -5t^2 + 20t
Here h is height in meters and t is time in seconds.
Share about maximum height reached by this ball!

Explanation- In the above solution, we observe that if we increase the value of 't' we get lower height. So the maximum possible height the ball could reach is h= 15 meters if we take t= 1 sec.
⚠️ Disclaimer: The cover image is created on Canva and rest of the images belong to me only.