SLC S22W4//Ecuaciones lineales y cuadráticas.

Portada diseñada con Canva
Tarea 1
Explicar la diferencia entre ecuaciones lineales y cuadráticas. Proporcionar ejemplos de cada tipo de sistema de ecuaciones y describir sus formas generales.
Ecuación lineal:
Es un tipo de ecuación algebraica formada por la suma y resta de una o varias incógnitas a la primera potencia. Es decir, que puede puede tener estar conformadas por una o varias incógnitas, pero dichas incógnitas sólo pueden sumarse o restarse entre sí.
Otra característica de estas ecuaciones es que las incógnitas o variables no pueden multiplicarse, ni tener exponentes, ni estar dentro de raíces, valores absolutos, logaritmos, entre otros.
Su representación gráfica es una linea recta, es por ello que se le llaman ecuaciones lineales.
Forma general:
ax + b = c
Donde:
a : coeficiente de x
b y c : coeficientes constantes.
Ejemplo:
Comenzamos el despeje de la variable y procedemos a pasar el numero 3 al lado derecho en forma negativa.
2x = 9 - 3
Resolvemos la resta.
2x = 6
Ahora procedemos a despejar la x, al pasar el 2 que estaba multiplicando a la variable x, quedando como divisor del lado derecho.
x = 6/2
De esta manera sabemos que el valor de x es 3.
x = 3
Ecuación cuadrática:
Una ecuación cuadráticas o también conocidas como ecuaciones de segundo grado son aquellas en la cual el exponente del término desconocido está elevado al cuadrado.
Su representación gráfica es una parábola, una curva en forma de "U".
Forma general:
ax² + bx + c = 0
Donde:
a, b y c son números reales, estos son conocidos como "coeficientes".
a es el coeficiente de x2,
b es el coeficiente de x
c es el término independiente.
Ejemplo:
3x² + 2x + 4 = 0
Siendo
a = 3
b = 2
c = 4
En base a esto, podemos establecer que la principalmente diferencia entre las ecuaciones lineales y cuadráticas se basan en el exponente de sus variables.
Puesto que en las ecuaciones lineales las incógnitas se elevan a la primera potencia, mientras que las incógnitas de las ecuaciones cuadráticas se elevan a la segunda potencia.
Tarea 2
Describir métodos para resolver ecuaciones cuadráticas y compartir pros y contras de cada método.
Método de factorización:
A través de la factorizacion, se busca expresar una ecuación cuadrática completa como el producto de binomios y de esta manera hallar el valor de x en cada binomio, asegurándonos de que satisfaga las ecuaciones.
Ejemplo:
x² - 7x + 10 = 0.
Al factorizar, se debe hallar dos números que al multiplicarnos den como resultado 10 y que a su vez, cuando se sumen den como resultado -7.
x² - 7x + 10 = (x ) . (x ) <--- Producto de 2 binomios
Los números que cumplen esta condición serian el -5 y -2.
x² - 7x + 10 = (x - 5) . (x-2)
Entonces igualamos a cero cada factor:
(x - 5) = 0
(x-2) = 0
Y finalmente, al despejar la x, obtenemos el siguiente resultado:
x = 5
x = 2
Ventaja: permite simplificar expresiones complejas a una expresión mas sencilla.
Desventajas:
No se puede aplicar en todas las ecuaciones, solo aquellas ecuaciones que sean factorizables por un término en común o aplicando un producto notable.
Se aplica solamente con números enteros que se pueden factorizar.
- Método de la fórmula cuadrática
La fórmula cuadrática se aplica para resolver cualquier ecuación que cumpla con la forma ax² + bx + c = 0.
Fórmula cuadrática:
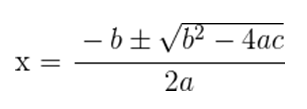
A través de la aplicación de esta formula, podemos obtener directamente las soluciones de una ecuación cuadrática.
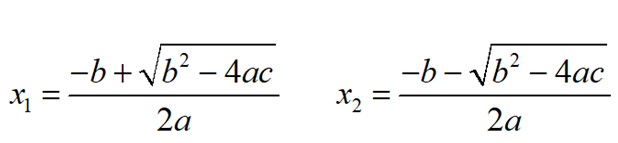
Es importante mencionar que este método se aplica para resolver ecuaciones cuadraticas que no se pueden factorizar.
Ejemplo:
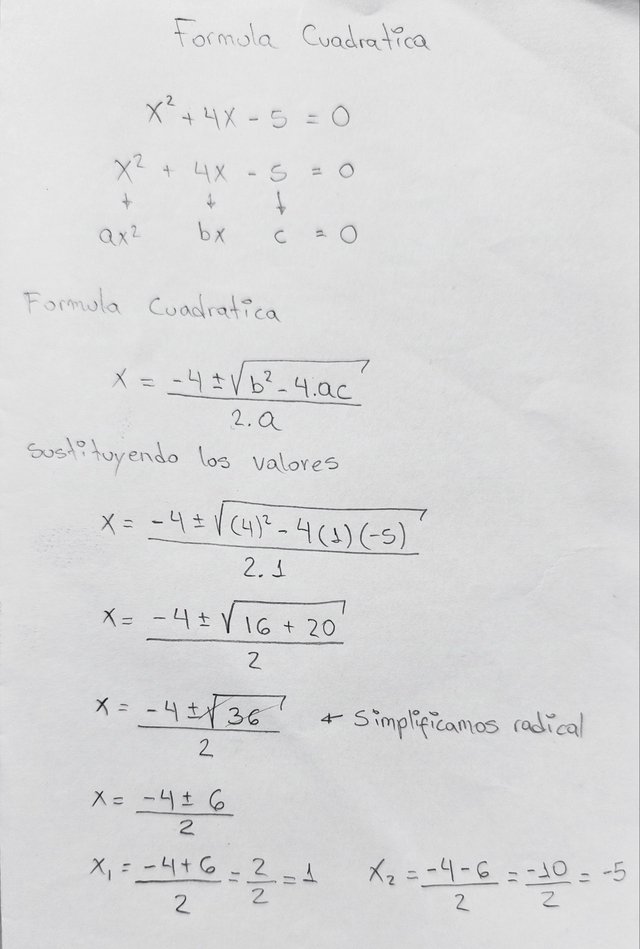
Ahora bien, procedemos a sustituir el valor de X con los resultados obtenidos previamente para verificar que son correctos.
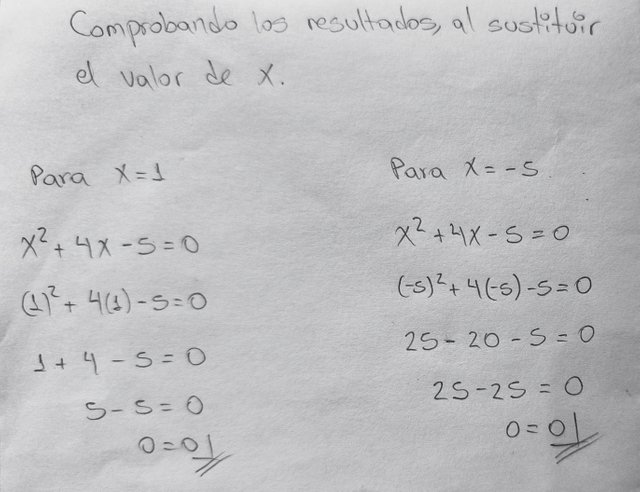
Ventaja:
- Permite resolver ecuaciones cuadráticas complejas que no se pueden factorizar.
Desventaja::
Solo se aplican a las ecuaciones que cumplen con la forma: ax² + bx + c = 0.
Se obtiene una o dos soluciones, y estas pueden ser números enteros o reales.
Método de graficación
A través de este método podemos representar gráficamente en un plano cartesiano a la la función cuadrática, en la cual se debe formar una parábola y de esta manera hallar los puntos donde la gráfica de la ecuación corta el eje x.
Este método permite visualizar las soluciones y analizar el comportamiento de la función cuadrática.
Ejemplo:
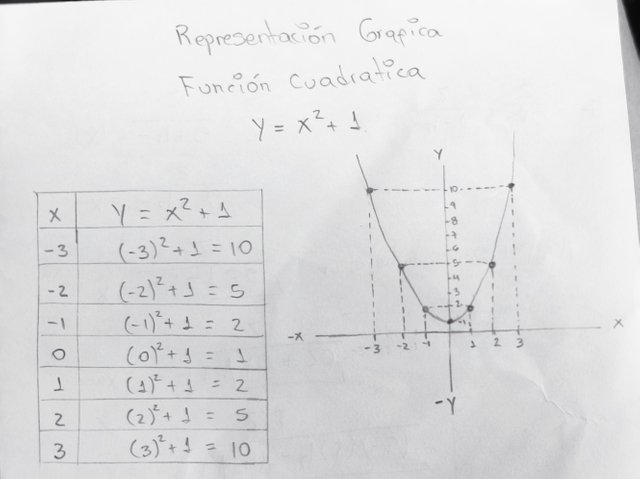
Ventaja:
- Fácil de visualizar e interpretar.
- Permite la comprobación de resultados de forma mas sencilla.
Desventaja:
- Requiere mas tiempo.
Tarea 3
Resolver la ecuación lineal 3x + 2 = 11 y mostrar el valor de x.
Para resolver esta ecuación lineal, debemos realizar el despeje de nuestra incógnita. Para ello debemos evaluar los componentes de la ecuación y en este caso lo mas apropiado es mover el numero 2 al lado derecho, este esta positivo, así que al trasladarlo al lado derecho se transforma en negativo.
3x + 2 = 11
3x = 11 - 2
Resolvemos la resta:
3x = 9
Luego continuamos despejando la X, por lo que trasladaremos el 3 que esta multiplicando a la X, al lado derecho dividiendo.
3x = 9
x = 9 / 3
Resolvemos la división y tenemos que:
x = 3

Resuelve esta ecuación cuadrática x² + 2x - 6 = 0.
Al evaluar la ecuación cuadrática x² + 2x - 6 = 0, vemos que cumple con la forma: ax² + bx + c = 0.
Por lo que es apropiado aplicar la formula cuadrática para resolver esta ecuación.
Fórmula cuadrática:
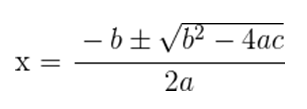
Ahora bien, procedemos a resolver la ecuacion:
x² + 2x - 6 = 0
Así que ahora debemos sustituir estos valores en la ecuación:
x = -2 ± √ (2)² - 4 (1) (-6) / 2 (1)
Resolvemos la potencia para ir eliminando paréntesis.
x = -2 ± √ 4 - 4 (1) (-6) / 2 (1)
Ahora resolvemos las operaciones de multiplicación.
x = -2 ± √ 4 - 4 (-6) / 2
x = -2 ± √ 4 + 24 / 2
Ahora, procedemos a resolver la operación de resta.
x = -2 ± √ 28 / 2

Continuamos, simplificando la expresión radical.
x = -2 ± √ 28 / 2
Entonces
√ 28 = 2√ 7
Quedando de la siguiente manera:
x = -2 ± 2√ 7 / 2
Ahora, podemos continuar resolviendo el valor de x.
x = -2 + 2√7 / 2
x = -1 + √7
x = 1,646
x = -2 - 2√ 7 / 2
x = -1 - √7
x = -3,646
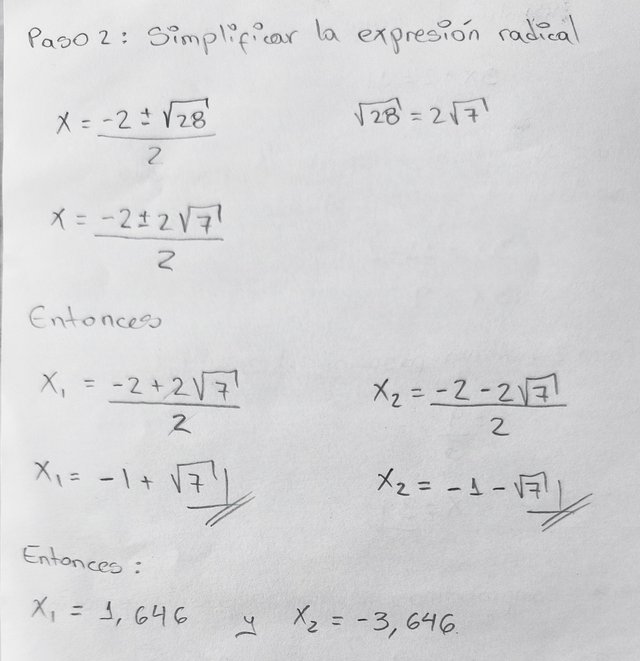
Finalmente procedemos a comprobar los resultados, sustituyendo el valor de x obtenido previamente en la ecuación.
x² + 2x - 6 = 0
Siendo x = 1,646 y x = -3,646
Entonces sustituimos el valor de x en la ecuacion:
x² + 2x - 6 = 0
Resolvemos la potencia:
(1,646 )² + 2 (1,646 ) - 6 = 0
Continuamos resolviendo la multiplicación:
2,709 + 3,292 - 6 = 0
Resolvemos la suma:
6 - 6 = 0
Y luego la resta:
0 = 0
De esta manera, comprobamos que el valor de x que hallamos previamente es correcto.
ahora, comprobamos el otro resultado.
x² + 2x - 6 = 0
Resolvemos la potencia:
(-3,646)² + 2 (-3,646 ) - 6 = 0
13,29 + 2 (-3,646 ) - 6 = 0
Continuamos resolviendo la multiplicación:
13,29 - 7,292 - 6 = 0
Resolvemos la suma:
13,29 - 13,29 = 0
Y luego la resta:
0 = 0
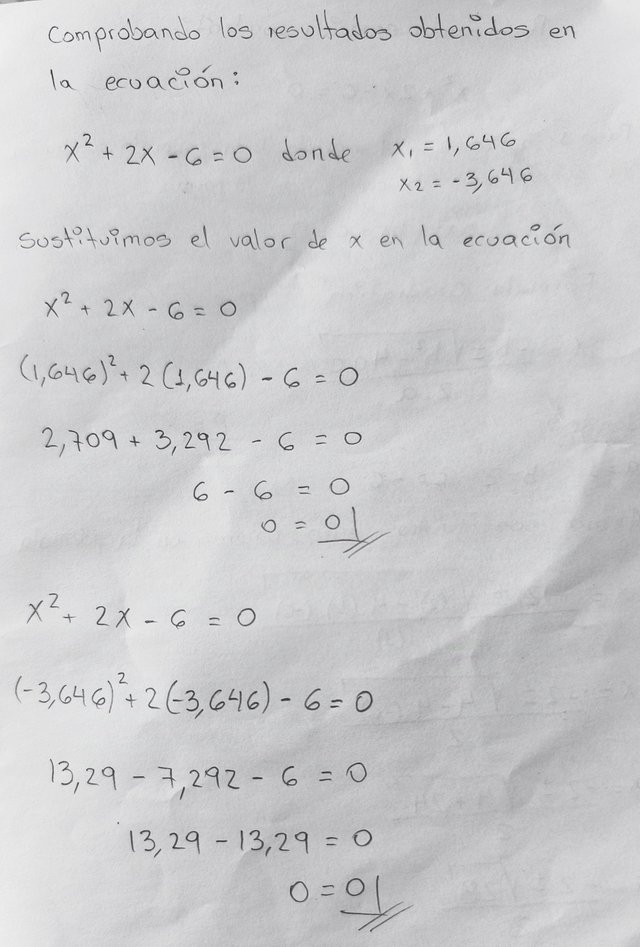
Tarea 4
Escenario número 1
Supongamos que Ali tiene 15 dólares para gastar en snacks. Compra un paquete de patatas fritas por 3 dólares. ¿Cuánto dinero le queda?
Supongamos que x es la cantidad de dinero que le queda a Ali.
Ecuación: x + 3 = 15
Comparte una solución para x

Escenario número 2
Supongamos que hay una pelota que se lanza en dirección ascendente desde el suelo con una velocidad inicial de 20 m/s y la altura de la pelota sobre el suelo se presenta mediante la siguiente ecuación:
h(t) = -5t² + 20t
Aquí h es la altura en metros y t es el tiempo en segundos.
¡Comparte sobre la altura máxima alcanzada por esta pelota!
El primer paso para lograr calcular la altura máxima alcanza, es determinando el tiempo, por lo que al visualizar esta expresión como una ecuación cuadrática de la siguiente forma:
h(t) = at² + bt + c
Así que realizamos el despeje de la incógnita (t), quedando de la siguiente manera:
t = -b/2a
Esta formula, nos permitirá calcular el tiempo en el que la pelota alcanza su altura máxima.
Ahora bien la ecuación viene dada de la siguiente manera:
h(t) = -5t² + 20t
Por lo que procedemos a sustituir los valores en la formula para calcular el tiempo:
t = -b/2a
t = -20 / 2(-5)
t = -20 / (-10)
t = 2 seg.

Ahora bien, conociendo el valor de (t), podemos calcular la altura máxima a traves de la siguiente ecuación:
h = -5t² + 20t
Siendo:
t = 2
Procedemos a sustituir el valor de t en la ecuación.
h(2) = -5(2)² + 20(2)
h(2) = -5(4) + 20(2)
h(2) = -20 + 20(2)
h(2) = -20 + 40
h(2) = 20

Hola mi querida amiga @ahumadaliliana29, un placer saludarte
Amiga me dejas sin palabras, excelente trabajo, se ve que dominas de atrás para adelante las matemáticas como diríamos en Venezuela.
Un trabajo bien extenso y dedicado, te felicito amiga, un buen trabajo y bien detallado. Gracias por tu amable invitación. Te deseo mucho éxito. Ese debe ser un 10. Dios te bendiga. Un abrazo 🤗