SLC-S22W3//Equations and Systems of equations

Equations and Systems of equations
Hello everyone. Happy New Year to you all. It's another week of learning challenge, year, contest, and I believe we are all excited To be dropping our amazing entries from which we can interact and learn from.
In this week's lesson, we will be discussing on equations and the system of equations which we generally see. Talking of equations we continue with algebra and other forms of algebraic equations. We didn't discuss in the last class. Involving the application in real life examples and problem solving.
Discuss on the difference between linear and non linear systems of equations. Provide examples of each type of system of equation and describe their general forms.
Mentioning of linear equation, all linear equations take the form of a straight line hence its name. A linear equation can take the general form of a straight line y- mx = c. Linear equations can go in two, three or more variables as illustrated below.
Linear equation in 2 variables.
ax + by = c------(1)
dx + ey = f-------(2)
Linear equation In 3 variables
ax + by + cz = d-------(1)
ex + fy + gz = h--------(2)
mx + ny + oz = p-------(3)
Common example
2x + 3y = 7
-x + y = 1
Nonlinear equation
These are system of equations in which at least one of the equation is not linear . Oh stop. These equations can take the form of a curves, parabola.etc.
These equations can take the form of a quadratic, explanation and trigonometric equations.
Common example
x² + y² = 25
y = x + 1
Key differences.
| Nature | Linear equation | Non Linear equation |
|---|---|---|
| Equation | All equations are straight lines | At least one equation is not linear |
| Graph | Intersection of two straight lines | Intersection of a line and a curve |
| Solution | Can be resolved using elimination ,substitution or graphical call method | Can be resolved using numerical method. |
It should be noted that both linear and nonlinear equations may have varying solution depending on the nature.
A System can have
Single solution: One touch at a single point.
Infinite solution: A line touches the curve at several points.
No solution: The line and the curve do not touch.
Discuss any one method for solving system of linear equations and share atleast one step by step algebric example.
Other than use of any of the three mention methods of solving linear equations, elimination, substitution and graphical methods, there is one more method of resolving linear equations in the same form. This method is no other method than the Matrix method.
Matrix method of solving linear equation
In order to resolve this, we are going to make use of the inverse property of a matrix And find the points from their image.
Consider The Matrix Equation MX = C
Where M represent The Matrix [(a,b),(c,d)]
X represent the points (x, y) And
C represents the image of the points (x', y')
Using the inverse property of a matrix, we can see that
X = M–¹C
Example
Solve the system of equation by matrix method.
2x + 3y = 8
x — 2y = -3
Solution.
Let M represent the Matrix.
M = [(2,3),(1,-2)]
The equation becomes
[2 3][x] = [8]
[1 –2][y]=[–3]
The first thing we do is look for the determinant of the Matrix M
Det[M] =( 2×(–2)) – (3×1)
= –4 –3
»» = –7
Adjoint [M] .
To look for the address of the Matrix M We interchange the elements of the leading diagonal, and reverse the sign of the minor diagonal. The Matrix become.
Adj [M] = [–2 –3]
[–1 2]
By stating the formula for the inverse we have.
M–¹ = 1/Det [M]× Adj M
M–¹ = 1/–7([–2 –3])
1/–7([–1 2])
To find the point x and y, We apply the already stipulated formula above.
X = M–¹C
We have
[x] = 1/–7([–2 –3])[8]
[y] = 1/–7([–1 2])[–3]
[x] = 1/–7[(–2×8)+(–3×–3)] = 1/–7[–16 +9]
= 1/–7(–7)
= 1
»» x = 1
[y] = 1/–7[(–1×8)+(2×–3)] = 1/–7[–8 + (–6)]
= 1/–7[–14]
= 2
»» y = 2
Concluding by Matrix method, for the system of equations. The solutions of x and y are (1, 2).
Solve the following system of linear equations:

To resolve this problem better, we are going to employ All the four methods of solving linear equations. Two for each case. So I still demonstrate a full application of how this can be done in real examples.
a) using graphical and Matrix method.
(I) Matrix method

(ii) Graphical method
 Derived coordinates
Derived coordinates
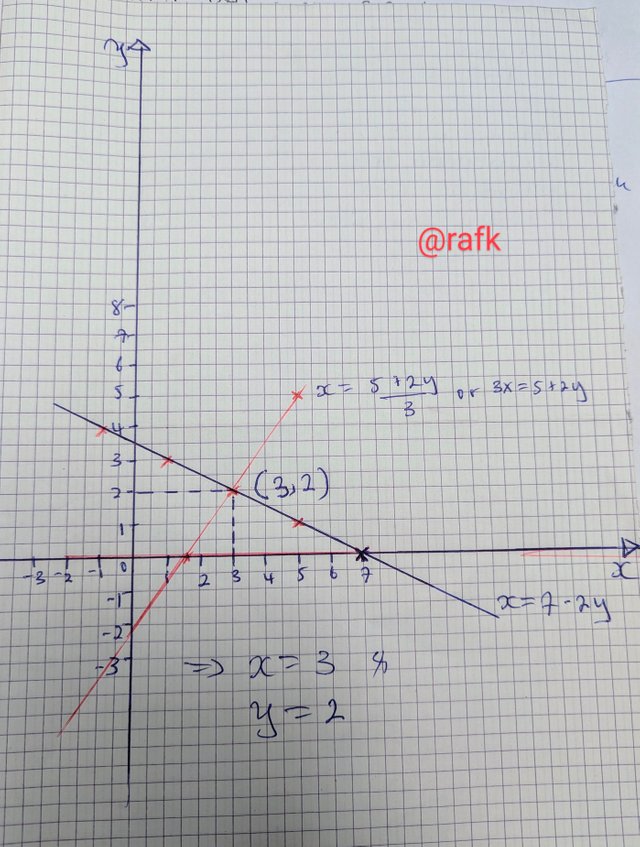
Graphical solution
Elaboration more on graphical method, The solution is a common point of intersection, Of the two lines. We can then get the solution of X and y from their various axis.
b) using using substitution and elimination method.
(I) Elimination method

(ii)

As we can you from my solution, whatever method we use and applying it correctly, we result to the same answers.
Task 4
Case number 1:

2x + 3y = 130 {cost of material}
x + 2y = 110 {cost of labor}
We are going to calculate the system of equations to see how much the company needs to produce in terms of cost of material and level labor.
2x + 3y = 130------(1)
x + 2y = 110 ------(2)
Using elimination method,
Multiply equation (2) by 2 Equation (1) by 1
2x + 3y = 130------(3)
2x + 4y = 220 ------(4)
Subtracting (4) - (3) Will results to
y = 90
Substituting the value of y In equation (2) We have
x + 180 = 110
»» x = -70
Analyzing, we can see that for the company to minimize boot cost and Labor, they need to produce - 70 units of A And 90 units of.
However- 70 units is not practical This suggests that the cost constraint in this case might not meet up with the production level.
To find the maximum production of B. Given that the constraint of production of 50 units of a exist can be carried out as follows.
Using equation 2
x + 2y = 110
50 + 2y = 110
2y = 60
y = 30
Therefore, if the company wish to produce 50 units of product A, The maximum number of product B they could produce while staying with the given cost. Constraint is 30 units. .
Case number 2:

x + 2y = 80 {cost of ingredients}
2x + y = 70 {cost of labor}
Resolving this system of equations by elimination methods,
x + 2y = 80-----(1)
2x + y = 70 -----(2)
Multiply equation ( 2) By -2
x + 2y = 80---------(3)
-4x –2y = -140 -----(4)
Adding equations
–3x = –60
»» x = 20
Substitute in the value of x in Equation (1)
20 + 2y = 80
2y = 60
»» y = 20
Interpreting, to minimize the cost of ingredients and labor, the bakery needs to produce 20 vanilla cakes and 30 chocolate cakes.
Now, if the company is reducing 30 vanilla cakes, the number of chocolate cakes they can produce staying in the given cost constraint is 30 chocolate cakes.
To further analyze, we see from calculation that the company was producing 20 vanilla cakes while Currently producing 30 chocolate cakes To minimize cost . Now if they want to increase their production of vanilla cakes to 30, they can still maintain The same number of chocolate cake which is 30 I'll still be in the same cost constraint.
Overall, it was an amazing lesson and I enjoyed it so much participating with interesting calculations and equally learning from the process. I would like to see some amazing persons share their own opinion and entries in this topic.
Best regards: @rafk.