SLC-S22W3//Equations and Systems of equations.

Photo taken from Pixabay
Hello everyone. Today I will take part in week 3 of Steem Learning Challenge, by @khursheedanwar. This week is focused on equations and systems of equations, you can find the original post here.
So, let's get started.


| Explain difference between linear and non linear systems of equations. Provide examples of each type of system of equation and describe their general forms. |
|---|
We know from the previous week that an equation can be described as a mathematical statement that declares the equality of two expressions, with one or more variables and constants and the use of the equal sign "=" between the expressions.
Now, a system of equations consists of multiple equations (typically two or more) that share variables. The goal is to find values for the variables that satisfy all the equations simultaneously.
| Linear Systems of Equations |
|---|
This type is described as linear because every variable can only be raised to a power of 1 and does NOT include trigonometric or exponential functions
The general form can be written as: a1x1 + a2x2 + ... + anxn = b. Where:
a1,a2,...,an are coefficients
x1,x2,...,xn are variables
b is the constant
The graph representation of a linear system is a straight line, a plane or hyperplane
The solution is a single point, a line or no solution
Example:
2x +3y = 8
x - 4y = -5
| Non-Linear Systems of Equations |
|---|
A system of equations is non-linear when there is at least one variable that has a bigger power than 1 or includes trigonometric or exponential functions
The general form can be written as:
f1(x1,x2,...,xn) = 0,
f2(x1,x2,...,xn) = 0, ...
Where: f1, f2, ... are non-linear functions
- The graph representation of a non-linear system can be circles, curves or other shapes
- The solutions represent points where all the graphs intersect, resulting in no solution, one or multiple solutions
Example:
x^2 + y^2 = 25
y = 2x^2
Key Differences:
| Type | Linear System | Non-linear System |
|---|---|---|
| Highest power | 1 | 2 |
| General form | variables appear to first power | variables may appear in power, products etc |
| Graph Representation | straight line, plane or hyperplane | circles, curves, parabolas, other shapes |
| Number of solutions | one, none, infinitely | none, one, multiple |


The method I chose for task 2 is Matrix Method, by using the idea of inverse matrices.
We can use matrices to represent a system of equations like this: AX = B, where:
- A is the matrix for coefficients
- X is the column matrix for variables
- B is the column matrix for constants
To solve for X, we need to first check if A is invertible and multiply both sides by A-1, which represents the inverse of A, to isolate X and get: X = A^-1 B which will give the solution.
Given a 2x2 matrix A, we can calculate the inverse of A, and also if it's invertible by using the formula:
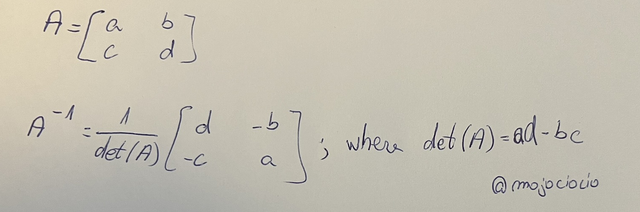
Now, let's take the following example and solve it using the Matrix Method:
2x + 3y = 8
x - 4y = -5
The first step is to write the matrices for A, B and X, and we will have:
A = |2 3|
|1 -4|
X = |x|
|y|
B = |8|
|-5|
And now the system becomes:
|2 3| |x| = |8 |
|1 -4| |y| |-5|
The next step, is to find the determinant of A so we can use it in the formula:
det(A) = (2)(-4) - (1)(3) = -8 - 3 = -11
Using this in the formula for inverse of A, we can write:
A^-1 = 1/det(A) |-4 -3| = -(1/11) |-4 -3| = |4/11 3/11|
|-1 2| |-1 2| |1/11 -2/11|
Now that we have the inverse of A, we can finally solve for X by using the formula mentioned above, X = A^-1 B:
X = A^-1 B = |4/11 3/11| * |8|
|1/11 -2/11| |5|
We then perform the multiplication like this:
X = |(4/11)(8) + (3/11)(-5)| = |32/11 - 15/11| = |17/11|
|(1/11)(8) + (-2/11)(-5)| |8/11 + 10/11| |18/11|
By interpreting the X matrix we can write the solution as: x = 17/11 and y = 18/11
The same solve for this can be found in the image below:



In this task, we have to solve 2 systems of linear equation. Let's start with the first one:
x + 2y = 7 (will note it as equation 1)
3x - 2y = 5 (will note it as equation 2)
The solve can be seen in the image below:

EXPLANATION
For this system, I chose the addition method.
- By adding the 2 equations together, we can get rid of the y variable and the resulting equation is:
4x = 12 - We can solve for x by simply diving the equation by 2 and getting that
x = 3. - Now, I will substitute
x = 3in equation 1 andx + 2y = 7becomes3 + 2y = 7. - Next step is to move the constant from the left side to the right and have
2y = 7 - 3 => 2y = 4 - We solve for y by diving by 2:
y = 2
The solution for this system is: x = 3 and y = 2
We can also do a verification of the solution by substituting them in both equations.
Equation 1:
3 + 4 = 7
7 = 7
TRUE
Equation 2:
9 + 4 = 5
5 = 5
TRUE

The second system of equations that we have to solve is:
4x + 6y = 2 (will note it as equation 1)
x - 2y = 3 (will note it as equation 2)
The solve can be found in the image:
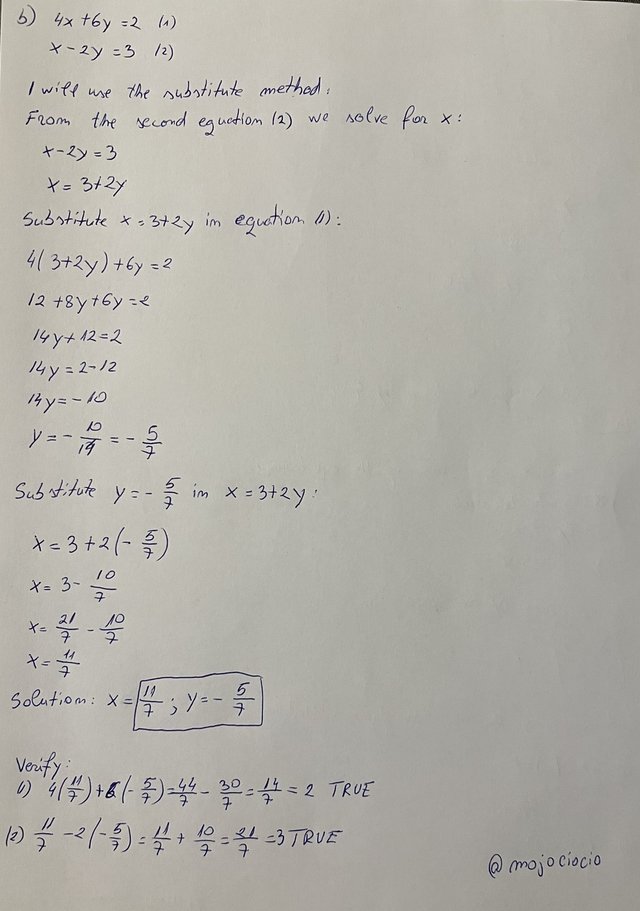
EXPLANATION
For this system, I chose the substitution method.
- First, I extracted x from equation 2 and have the expression for x:
x - 2y = 3 => x = 3 + 2y
- Next step is to substitute
x = 3 + 2yin equation 1 to get this equation:4(3 + 2y) + 6y = 2 - We solve this by first multiplying the parenthesis and get:
12 + 8y + 6y = 2 - By adding the coefficients of the variable we have:
12 + 14y = 2 - We move the constant on the right side so the variable is alone:
14y = 2 - 12 => 14y = -10 - Solve for y and get:
y = -(10/14) => y = -(5/7) - Next, we substitute
y = -(5/7)in the expression of x:x = 3 + 2[-(5/7)]and getx + 3 - (10/7) - We can write 3 as 21/7 so we have:
x = 21/7 - 10/7 => x = 11/7
The solution of the system is: ```x = 11/7 and y = -(5/7)``. Let's verify it:
Equation 1:
44/7 - 30/7 = 2
14/7 = 2
2 = 2
TRUE
Equation 2:
11/7 + 10/7 = 3
21/7 = 3
3 = 3
TRUE


Scenario 1
| Suppose there's a company producing two products, A and B.If cost of producing x units of A and y units of B is given by system then; 2x + 3y = 130 (cost of materials); x + 2y = 110 (cost of labor). If company wants for producing 50 units of product A then calculate how much units of product B they may produce? |
|---|
We are given the system of equation:
2x + 3y = 130 (will note it as equation 1)
x + 2y = 110 (will note it as equation 2)
And that x = 50
With this information, we can substitute x = 50 in equation 1 and solve it:
2(50) + 3y = 130
100 + 3y = 130
3y = 130 - 100
3y = 30
y = 10
From the first equation, we get y = 10.
Also substitute x = 50 in equation 2 to check if we get the same result for y:
50 + 2y = 110
2y = 110 - 50
2y = 60
y = 30
From the first equation, we get y = 30.
We can see that we get conflicted results for y from resolving the 2 equations. From the 1st one we get y = 10 and from the 2nd one we get y = 30. Given this, we can say that the system is INCONSISTENT and there is no solution for it.


Scenario 2
| Suppose there's a bakery producing two types of cakes which are vanilla and chocolate. If cost of producing x cakes of vanilla and y cakes of chocolate is given by system then; x + 2y = 80 (cost of ingredients)2x + y = 70 (cost of labor). If bakery wants for producing 30 cakes of vanilla then calculate how much cakes of chocolate can they produce? |
|---|
We are given the system of equation:
x + 2y = 80 (will note it as equation 1)
2x + y = 70 (will note it as equation 2)
And that x = 30
Again, we start the solve by substituting x = 30 in equation 1 to get a value for y:
30 + 2y = 80
2y = 80 - 30
2y = 50
y = 25
From the first equation, we get y = 25.
Substituting x = 30 in equation 2, we get verify the value for y:
2(30) + y = 70
60 + y = 70
y = 70 - 60
y = 10
From the first equation, we get y = 10.
Resolving the system of equations, we get 2 different values for y when x = 30. This means that the provided system is is INCONSISTENT and there is no solution for it.


As always, thank you for reading and I'd like to extend an invitation to @ady-was-here, @radudangratian and @cmalescov to take part in this.