"SLC-S22W3//Equations and Systems of equations."
I am @hudamalik20 from Pakistan. How are you all ?. I hope you all are well and doing great in your life .Today I am participating in this "SLC-S22W3//Equations and Systems of equations." organized by @khursheedanwar w.So let's start.


• Task 1
• Explain difference between linear and non linear systems of equations. Provide examples of each type of system of equation and describe their general forms.
Linear Systems of Equations:
A linear system refers to a system of equations in which each equation is linear. This means that the variables appear onluy to the first power and are not multiplied or divided by each other. In a llinear system, the equatons represent straight lines when plotted on a graph.
The general form of a linear equation in two variables x and y is:
Ax + By = C

For example,let me consider the following system of equations:
x + 2y = 7
3x - 2y = 5
Both of these equations are linear because the variables x and y are raised to the first power and are not multipllied by each other. And these equations represent straight lines when plotted on a graph.
Non-Linear Systems of Equations:
A non-linear system refers to a system of equations in which at least on equation is not linear. This means that at least one of the equations contains termms where the variables are raised to powers greater than one (such as x^2,y^2 ) or involve other functions like logarithms or trigonometric functions.

The general form of a non-linear equation can include terms like x^2, y^2, or xy . An example of a non-linear equation could be:
x^2 + y^2 = 25

• Task 2
• Describe any one method for solving system of linear equations and share atleast one step by step algebric example.
For this task, I will be solving a system of linear equations using Cramer's Rule, which is different from the substitution, elimination, and graphing methods. Andy his method is useful when there are multiple variables in the equations, like I took two or more, and it applies to systems where the number of equations equals the number of variables.
The important thing to remember when using Cramer's Rule is that we must first ensure the coefficient matrix has a non- zero determinant so we first check this otherwise, the system won’t have a unique solution and can't be solved using this method.
The basic process involves working with matrices. We can write the system of linear equations in matrix form, which allows us to perform operations using determinants. If the determinant of the coefficient matrix is non zero, we can solve for the unknowns by finding the determinants of modified matrices.
Steps for solving using Cramer's rule
So let me consider a system of two liner equations ...
a1x+b2y=c1
a2x+b2y=c2




So now I represent this equation in matrix form.
| 1 1 1 |R1
| 1 1 1|R2
Then we write the coefficient matrix
We calculate the determinant of the coefficient matrix ..
| a1 b1 |
| a2 b2 | = (a1.b2-a2.b1)
Now we replace the first column of A with the constants from the right hand side of the equation....
Dx = | c1 b1 |
| c2 b2 | =
(c1.b2-c2.b1)
Then we replace the second column of A with the constants from the right hand side of the equations ...
Ay= | a1 c1 |
| a2 c2 | = (a1.c1-a2.c2)
After the calculation we find the values of x and y ...
x = Dx/D , y=Dy/D

• Task 3
• You need for solving following system of linear equations:
(a)
x + 2y = 7
3x - 2y = 5

(b)
4x + 6y = 2
x - 2y = 3
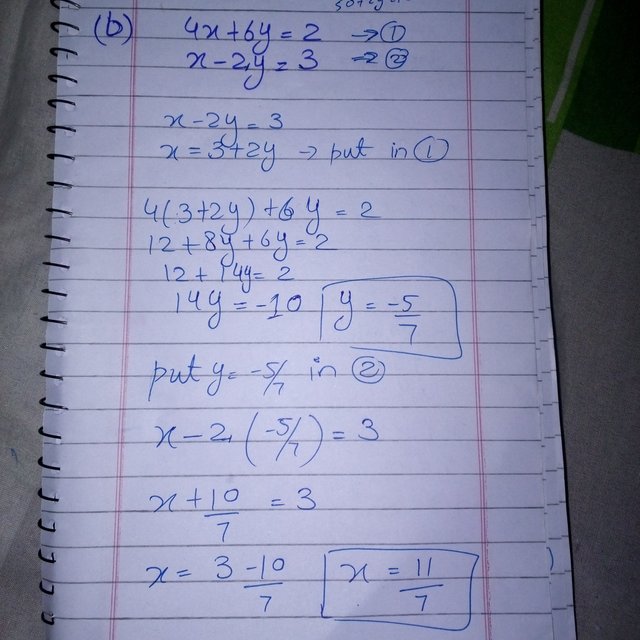

• Task 4
Scenario number 1
Suppose there's a company producing two products, A and B.If cost of producing x units of A and y units of B is given by system then;
2x + 3y = 130 (cost of materials)
x + 2y = 110 (cost of labor)
We’re given two equations:
- 2x+3y =130 so this is for the cost of materials.
- x+2y=110 so this is for the cost of labor.
Here, x is the number of Product A units, and y is the number of Product B units.
So the company wants to make 50 units of Product A. So, I’ll take the second equation:
x + 2y = 110
50 + 2y = 110
2y = 110 - 50
2y = 60
y = 30
Answer: So now I know that the company can make 30 units of Product B.
Scenario number 2
• Suppose there's a bakery producing two types of cakes which are vanilla and chocolate.If cost of producing x cakes of vanilla and y cakes of chocolate is given by system then;
.x + 2y = 80 (cost of ingredients)
2x + y = 70 (cost of labor)
Now, we have another set of equations:
- x + 2y = 80 so this is for ost of ingredients
- 2x + y = 70 so this is for cost of labor..
Now here, x is the number of vanilla cakes, and y is the number of chocolate cakes.
The bakery decides to make 30 vanilla cakes. So, I’ll take the first equation:
x + 2y = 80
30 + 2y = 80
2y = 80 - 30
2y = 50
y = 25
Answer: So thhe bakery can make 25 chocolate cakes..
Now that's it from today's blog I hope you will like it. With best wishes ❤️. Now I like to invite @tammana, @pathanapsana and @norat to participate in this amazing contest.
Thanks alot for reading ❤️🤗 .
