SLC-S22W2/Equations and inequalities."

Hello guys.

Welcome to my blog. So excited to have you participate with me on this amazing learning challenge. Only for this time, we have been brought an amazing topic to discuss on, equations and inequalities. One of my best in fact my subject, I should have a lot to say about this.

Not wasting much time let's begin.

Equations are a combination of variables (components/character) and coefficients (numbers). Equations exist in many different form and categorize in different approach. In this scope we will be discussing mainly on equations involving algebra.

Difference Between Linear and Quadratic Equations

Linear and quadratic equations are two fundamental types of algebraic equations, but they differ in their degree, graph representation, and solutions.

---

Explain difference between linear and quadratic equations. Provide examples of each type of equation and describe their general forms.

---

Linear and quality equations are represent algebra falling under the category of polynomials. There is so much similarity and difference as well. Listing them side by side, we can say this about them. Polynomials derived their name depending on the highest degree of the in the variable

Linear equation.

These are classes of equations with the highest degree of in the main variable as 1. All linear equations take The general form representation of a straight line ax + b =0 where a and b are constant coefficients.

Linear equations represent straight line graphs that cuts across curves on the Cartesian axes.

Examples : 2x+1= 0

Quadratic equation.

A quadratic equation is an In which the highest power of the variable is 2. They are often referred to us. Trinomials. Meaning they have three terms. The general form representation of quadratic equation is ax² + bx + C =0. a , b and c representint coefficients of variables

Example: x²- x - 6= 0

Quality equations represent the locus of a parabola and usually described a u-shape or n-shape. The value of The coefficient of x² determines the shape of the curve using the general question ax² + bx + C =0, If the value of a is less than 0, The curve is n-shape. If the value of a is less than 0, The curve is u-shaped.

Here is a Tabular representation of the differences between linear equations and quadratic equations.

---

Features	Linear equation	Quadratic Equation
General form	ax + b = 0	ax² + bx + C =0
Degree	1	2
Graph	straight line	parabola
Solution	one solution	two solution
Example	2x+1= 0	x²- x - 6= 0

---

Real life application.

Linear equation:

Example: A taxi charges a base fare of $5 and an additional $2 per kilometer. Write a linear equation representing the total fare and calculate the fare for a 10 km ride.

Quadratic Equation.

Example: A ball is strong vertically upward and the path described by the ball is modeled by the equation of its height from position of throw as

H= 2t² + 5t +3

Determination the balls height after 2 seconds have passed.

---

Describe two different types of inequalities(Which are not explained in course). Provide examples of each type of inequality and explain how to solve them.

---

Symbol used: < > <= >=

Before beginning with inequalities, I am pretty sure we must have gone through the first stages of inequalities starting with linear inequalities, combined inequalities.

Proceeding to different type of inequalities, these inequalities can be resolved using different methods and approach. In the main lesson, the first two type of inequalities were discussed and now we will be discussing on something different.

Quadratic inequalities.

These type of inequalities are modeled from the quadratic equation for stop. It's simply removing zero from the right hand side of the aquatic equation and replacing it with an inequality symbol.

Take for instance the general from representation of a quadratic equation, ax² + bx + C =0 It can be transformed into an inequality as such; ax² + bx + C <0,
ax² + bx + C >0.

To resolve this type of inequalities, there are two methods to go about it. Either by using the sign table or graphically. We are going to take one example and solve it using the both method.

Sign table method

Example. Solve the quadratic inequality x² - x - 6 < 0.

Solution

The easy way to do this is to start by factorizing the right hand side of the equation. I believe we have come across the main lesson and see how we can factorize an equation using the zero product theorem.

x² - x - 6 < 0.

Let's look for the factors of - 6 When multiplied will give - 6, and when added will give -1.

Listing: 1,-1, 2,-2, 3,-3, 6,-6. Observing, our factors are highlighted as follows. The equation transform to.

( x² + 2x)- (3x- 6 )< 0.. factorized by grouping.

x(x+2) - 3(x+2) < 0

(x +2)(x - 3) < 0

Zeros of the equation are (- 2, 3)

stating the range:

x < -2 , -2 < x < 3, x > 3.

Sign table .

-	x < -2	-2 < x < 3	x > 3
x	- 3	2	4
(x +2)	-	+	+
(x - 3)	-	-	+
(x +2)(x - 3)	+	-	+
Sign		✓

::• The solution that satisfy the inequality is the range
-2 < x < 3
Explanation:
The X values are the values directly representing the range. Values below -2, between -2. And 3 And above 3.

Substituting the values of X in the linear equations, only design is noted. As we all know, all values below zero are negative. Multiplying the signs and getting the final sign. Which is zero satisfied inequality.

Note: To resolve the same inequality graphically we plot the graph and where the curve cuts. The x-axis represent the solution which satisfies the inequality and this is the region below the zero line.( -2 < x < 3).

Absolute value inequalities

Absolute value inequalities are inequalities with the magnitude sign attributed to it. It can be linear or quadratic depending on the inequality we are working with. Let's have a look at this type of inequality and how it can be resolved.

Example: Resolve the inequality.

|2x -5|<=7

Solution.

There are two approach of resolving this. Theory States that the magnitude sign cancels out any negative, so it's simply a symbolic+ or -. So we can separate the equation as such and solve them independently and have a unique solution by using the number line.

Another way to do this is to square both side of equation to get away with the magnitude sign and then resolve it. Quadratically using the sign diagram.

Let's begin with the first method.

|2x -5|<=7

+

(2x -5)<=7. Removing the brackets,

2x -5<=7.
Balance the equation by adding 5 on both side of the equation from both sides.

2x -5+5<=7+5.

2x <= 12.
Divide both side of the equation by 2.

x <= 6.

---

-

-(2x -5)<=7

Opening the bracket and multiplying the negative if the content inside, we have.

-2x + 5 <=7.

Subtracting 5 from both side of the equation, we have

-2x + 5 - 5 <=7- 5

-2x <= 2
multiplying both sides of the equation By -1 first, transform the equation to.

2x >= -2.

We can picture the sign changed. Meaning the operation have been reversed. Divide both side of the equation by 2 constraint.

x >= -1

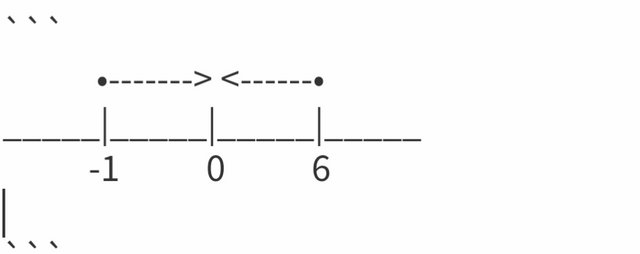^{On a number line}

Also, we can see that the The dots. I bold(•). Indicating that the point is included <=/>=. If it is strictly less than < or greater > than we will have an empty cycle (°).

Seems the graphs are moving in opposite direction. The common solution between them is represented by.

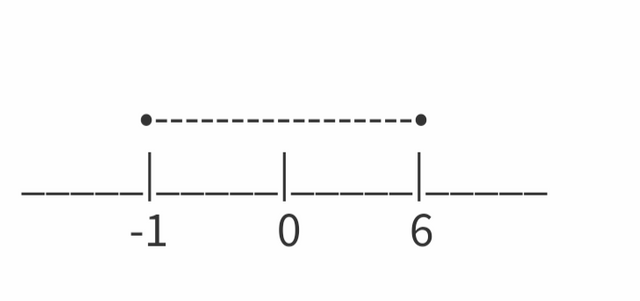
Which is the region between- 1 and 6.

The solution to the inequality is-1<= x <= 6

---

Method 2.

(2x -5)²<=(7)²

Square in both sides of the equation, remove the magnitude sign.
. Expanding and bringing light terms together we can change the equation to.

4x² - 20x + 25 <= 49

Subtracting 25 from both side of the equation,

4x² - 20x + 25 - 25 <= 49 - 25

4x² - 20x <= 24

Subtracting 24 from both side of the equation, we have

4x² - 20x - 24 <= 24 - 24

4x² - 20x - 24 <= 0

4 is coming here. So we divide All through by 4.

x² - 5x - 6 <= 0

Which becomes a linear quadratic equation.

Before we mention of graphical solution, let's resolve this one using the graphical method.

Let y equals to the inequality.

y = x² - 5x - 6

Step 1.

Locate the intercepts of the X and the y axis.

At x, y= 0.

,=={>

===> x² - 5x - 6 = 0

(x+1)(x-6)=0

x = - 1 or x = 6 point are (-1, 0 ) & (6, 0)

At the y-intercept, x = 0 ,

y= 0 - 0 - 6 = -6 points, (0, -6)

Coordinates of turning point.

The general form representation of a quadratic equation is given of the form. ax² +bc + c = 0. Observing.

Coordinates of the turning point.

The coordinate of the turning point are given by.

(-b/2a, (4ac - b²)/4a) ===>. (--5/2(1), [4(1)(-6) - (-5)²]/4)

T.p (5/2, -49/4)

The rest is for us to plot and choose the region which satisfy the equation.

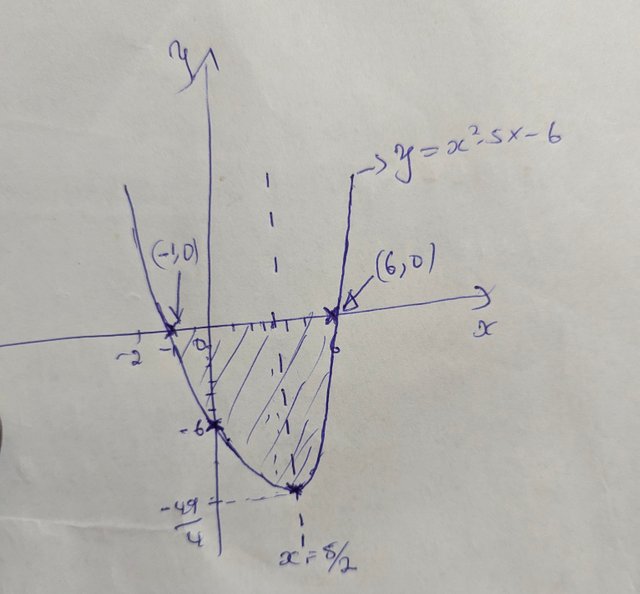
In the image above, we can see that the graph cut the x-axis at -1 and 6 and the shaded region represents the common solution to the inequality graphically.

Therefore-1<=x<=6 is the solution to the inequality graphically..

---

Solve the following linear equation: 2x + 5 = 11.Show step-by-step solution and share its practical example of how this equation can be applied in real life scenario.

---

Solve the equation. 2x + 5 = 11.

Solution.

Step 1. Isolate constant terms from variables.

Take away 5 on each side of the equation.

2x + 5-5 = 11-5

2x = 6

step 2.

Divide both side of the equation by the constant of the variable.

2x/2 = 6/2

x = 3.

::• The solution to the equation is. x =3

---

Real life application.

A taxi charges a base fare of $5 and an additional $2 per kilometer. Given that the total fare is $ 11 for a particular ride, calculate the fare
Per a ride.

**Solution. **

Let x = kilometers

Extra $2 per kilometers= 2x

Base far = $5

Total fare = $11.

But total fare = base fare + extra charge per kilometers.

==> 2x + 5 = 11

Subtracting $5 each we have

2x = (11 - 5)

2x = 6

Divide by 2

x = 3

Therefore

For a kilometer he charges $3 each.

---

4

---

---

Equation

Analysis.

Ingredients required per cake.

• 2 cups of flour.
• 1 cup of sugar..
• 0.5 cup of cocco powder.

Available ingredients to be used.

• 10 cups of flour
• 8 cups of sugar and
• 4 cups of cocoa powder.

Number of cake per ingredients

• flour
  2 cups of flour for 1 cake.

10 cups of flour for x cakes

==> X = 10/2 = 5 cakes to be made

• sugar.
  1 cups of sugar for 1 cake.

8 cups of sugar for x cakes

==> X = 8/1 = 8 cakes

• cocoa powder.
  0.5 cups of cocoa powder for 1 cake.

4 cups of cocoa powder for x cakes

==> X = 4/0.5 = 8 cakes.

Analysis conclusion.

It would have been possible to make a maximum of eight cakes if the ingredients measure up are the same level. But since the quantity of four Is limited, big Target of eight cakes would not be possible, to talk of 6 even.

So Tom can only make maximum of 5 cakes with the available resources. Therefore x = 5 cakes.

---

Inequalities

Let X represent the number of cakes Tom wants to make

• flour

2x <= 10

• sugar

1x <= 8

• Cocoa powder

0.5x <= 4

• at least 6 cakes

x>= 6

Analysis.

With the available resources, Tom is capable to making at least 6 cakes.

For the available resources, x !<=5 but x>= 6 Is a favorite condition.

Now for sugar/ cocoa powder, x <= 8.

So they took conditions for this to be possible is

{x>= 6,
{ x <= 8.

Representing these two solutions on a number line, the following conditions will be satisfied.
6 <= x <= 8. Which is the command region that satisfied it to inequalities.

---

4b

---

Solution

Let x represent number of gallons Ashley can purchase.

Distance between two city = 240 miles

Consumption = 1 Gallon /20 mile.

Using the already given inequality,

x + 2 >= 240/20 - 1

240/20 = 12 gallons

==> x + 2 >= 12 -1

The equation transform to

x + 2 >= 11

Subtraction of 2 on either sides

x + 2 - 2 >= 11 - 2

x >= 9

Concluding, Ashley will have to purchase at least 9 gallons of gas to reach city be and be left with 1 gallon extra.

Behold, it was an amazing lesson and I enjoyed practicing on it. At this point, I would like to invite the following persons to join me with their entry on this amazing challenge.

@chant

@wirngo

@simonnwigwe

---

---

Credit to: @rafk.

---