SLC-S22W2/Equations and inequalities
Hello everyone and welcome to my participation post in the second week of the Algebra Challenge, organized by @khursheedanwar. This week's challenge focuses on Equations and inequalities. You can find the contest here.

Edited by Canva, original photo from Pixabay
An equation can be described as a mathematical statement that declares the equality of two expressions. It usually contains one or more variables and constants and uses the equal sign "=" to show that the expressions are equal. The general form can be written as "Expression 1 = Expression 2". Algebraic example: 2x + 5 = 9.
On the opposite side, we have inequalities. These are used to compare two expressions using the inequality symbols. It can be represented by one of these symbols: >, <, ≥, ≤. The general form: "Expression 1 (symbol) Expression 2". Algebraic example: 3x - 4 > 5.
Now let's get on with the homework tasks.
Task 1
| Explain difference between linear and quadratic equations. Provide examples of each type of equation and describe their general forms. |
|---|
Before we can explain the differences between these 2 types of equations, we first need to understand them. Both of them are fundamental types of algebraic equations, each with it's own characteristics.
Let's take linear equations. This type can be defined as an equation in which the highest power a variable can have is 1. The general form can be written as: ax + b = 0, where a and b are constants, a cannot be equal to 0 and x is the variable. This type of equation has exactly one solution. The graph representation of a linear equation is a straight line.
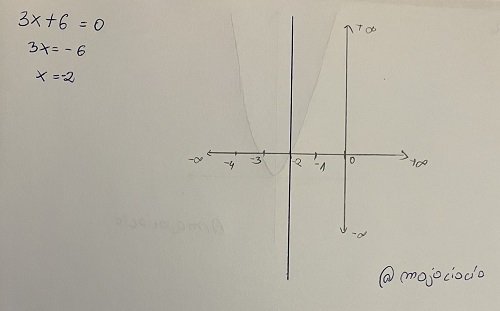
Graph representation of linear equation
An algebraic example: 2x + 3 = 0.
Let's consider the following practical example: Alex has $15 to buy pens, each pen is $3. If he wants to buy 4 pens, how much money is he left with?
We can write the equation like this: 3 * 4 + y = 15, where y is the amount of money he is left with. After the multiplication, the equation becomes: 12 + y = 15. We subtract 12 from both sides and we get: y = 3. So, after buying 4 pens at a price of $3 per pen, he is left with $3.
Now, let's talk about the quadratic equation. This equation type represents an equation where the highest power of a variable is 2. The general form is: ax2 + bx + c = 0, where a, b and c are constants, a is be equal to 0, and x is the variable. This type of equation can have up to two solutions, real of complex. The graph for quadratic equation is a parabola (U shaped curve).
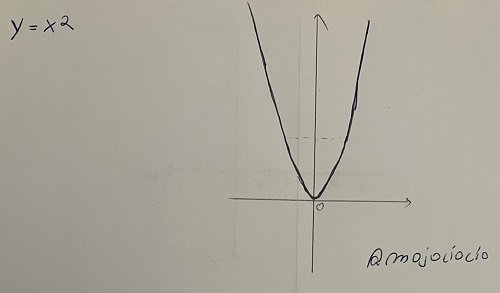
Graph representation of quadratic equation
An algebraic example: x2 - 2x + 1 = 0.
For a practical example, we can consider:
So, we can compile a table and present the key differences between the 2 types of equations:
| Key feature | Linear Equation | Quadratic Equation |
|---|---|---|
| Highest power | 1 | 2 |
| General form | ax + b = 0, where a ≠ 0 | ax² + bx + c = 0, where a ≠ 0 |
| Graph Representation | Straigth line | Parabola |
| Number of solutions | exactly one solution | up to two solutions |
Task 2
| Describe two different types of inequalities. Provide examples of each type of inequality and explain how to solve them. |
|---|
The 2 types I chose for this task are: Quadratic Inequalities and Absolute Value Inequalities.
A Quadratic Inequality involves a quadratic expression, usually taking one of these forms: ax² + bx + c < 0, ax² + bx + c ≤ 0, ax² + bx + c > 0, ax² + bx + c ≥ 0, where a, b, and c are constants.
Let's take this as an example: x² − 4x + 3 ≥ 0.
- First step is to factor the quadratic: x² − 4x + 3 = (x - 1)(x - 3)
- Next, we set the factor to 0 to find the roots: (x - 1)(x - 3) = 0. This gives us x - 1 = 0 = > x = 1 and x - 3 = 0 = > x = 3.
We need to determine the sign of the expression for each interval like this:
- For 𝑥 < 1, we can test a value of x = 0: (0 - 1)(0 - 3) = 3 > 0
- For 1 < x < 3, we can consider x = 2: (2 - 1)(2 - 3) = - 1 < 0
- For x > 3, let's say x = 4: (4 - 1)(4 - 3) = 3 > 0
All these steps, will give us this solution: (-∞, 1] U [3, ∞)
For the second type of inequality, I chose Absolute Value Inequalities. This model involves inequalities with absolute value symbols "| |". This value represents the distance from zero on the number line and it's always positive.
Example: |x - 3| < 5. To solve this, we use these steps:
- write the equivalent compound inequality: -5 < x - 3 < 5
- solve for x by adding 3 to all sides: -2 < x < 8
- the solution is the interval (-2, 8)
Task 3
| Solve the following linear equation: 2x + 5 = 11. Show step-by-step solution and share its practical example |
|---|
The first step in solving the given linear equation is to isolate the variable term. To do this, we must subtract "5" from both sides, as shown in the image below:

Step 1
The second step, is to solve for x. In our case, we need to divide both sides by 2

Step 2
This will give us the final answer, which is x = 3:
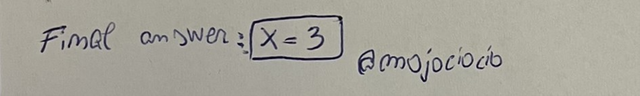
Final answer
Task 4
| Scenario 1: Tom's Bakery |
|---|
For this scenario, we are tasked with calculating the number of cakes that can be made by Tom, having information about the amount of ingredients he has.
| Equation |
|---|
To start this task, we need to analyze the given data. We are told that Tom has:
- 10 cups of flour
- 8 cups of sugar
- 4 cups of cocoa powder
We also know, that a cake requires:
- 2 cups of flour
- 1 cup of sugar
- 1/2 cup of cocoa powder
Using this given information, we can write our equation and find out how many cakes can Tom make from his ingredients.
- With the amount of flour, he can make: 2x = 10. Which gives us x = 5. So Tom can make 5 cakes with his amount.
- The amount of sugar will make: 1x = 8; x = 8. He has enough sugar for 8 cakes
- As for the coca powder, (1/2)x = 4; and by multiplying each side by 2 we get x = 8. Tom can make 8 cakes with this amount of cocoa powder
Analyzing the equation results, we can see that even if he has enough sugar and cocoa powder for 8 cakes, he only has enough flour for 5. So the answer is: he can make 5 cakes
| Inequality |
|---|
Tom wants to ensure he has sufficient sugar for at least 6 cakes and we know that each cake needs 1 cup of sugar, while Tom has 8 cups.
- We can write the inequality for the total sugar needed for x cakes like this: 1x ≤ 8.
- He wants to make at least 6 cakes, so the inequality is: x ≥ 6
By combining the 2 limitations we obtain the following inequation: 6 ≤ x ≤ 8. Tom can make between 6 and 8 cakes, since the sugar is the limiting factor
| Scenario 2: Number of gallons Ashley needs |
|---|
Similar to before, for this scenario we need to calculate the number of gallon of gas Ashley needs for the road trip from City A to City B. To do this, we need to breakdown the task.
- The distance between City A and City B is 240 miles
- The fuel efficiency of the car: 20 miles per gallon
- Fuel tank capacity: 12 gallons
- Current fuel available in the tank: 2 gallons
| Inequality |
|---|
We have: x + 2 ≥ (240/20) - 1, where x is the number of gallons of gas Ashley can buy. To solve this we can follow these steps:
- first do the parenthesis: 240/20 which gives us 12.
- now, the inequality becomes: x + 2 ≥ 12 - 1
- now we do the subtraction on the right side of the inequality: 12 -1 = 11. The inequality is: x + 2 ≥ 11
- substract 2 from both sides, and we get x ≥ 9
This means, that the number of gallons Ashley needs to buy is at least 9
As always, thank you for reading and I'd like to extend an invitation to @ady-was-here, @radudangratian and @cmalescov to take part in this.