SLC-S22W2/Equations and inequalities

Hello steemians,
Task 1: Explain difference between linear and quadratic equations. Provide examples of each type of equation and describe their general forms.
Linear equation
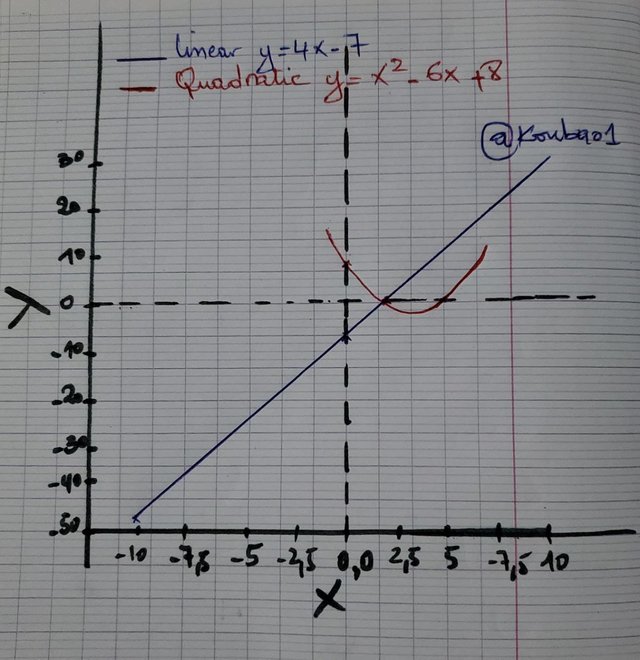
A linear equation is one where the maximum power of the variable is 1. It models a proportional or constant relationship between variables, graphically, it forms a straight line.
The general form is ( ax + b = c ), where ( a ), ( b ), and ( c ) are constants, and ( x ) is the independent variable.
For example, take the equation (4x - 7 = 9), to solve it, we add 7 to both sides to get (4x = 16), then divide by 4 to get (x = 4),
A practical example would be a taxi charging $7 in fixed costs plus $4 per kilometer, if the total cost of a journey is $9, the equation (4x - 7 = 9) allows us to find that the taxi has walked 4 kilometers.
Quadratic Equation
A quadratic equation is one where the maximum power of the variable is 2. It is used to model phenomena such as the movement of an object or the trajectory of a ball. Graphically, it forms a parable.
The general form is (ax^2 + bx + c = 0), where (a), (b), and (c) are constants, and (x) is the variable independently.
Take the example ( x^2 - 6x + 8 = 0 ), to solve this equation, we factor: ( (x - 2)(x - 4) = 0 ), the solutions are ( x = 2 ) and ( x = 4 ).
A practical example would be a ball launched vertically with an initial speed of 30 m/s from a height of 5 m, the height of the ball after ( t ) seconds is given by ( h(t) = -4.9t^2 + 30t + 5 ), to determine when the ball hits the ground (( h = 0 )), we solve a quadratic equation.
Linear and quadratic equations differ in their structure, their maximum power of the variable, and their graphing. A linear equation has a maximum power of 1 and forms a straight line, while a quadratic equation has a maximum power of 2 and forms a parable.
The above graph illustrates these differences: a straight line for the equation ( y = 4x - 7 ) and a parabola for the equation ( y = x^2 - 6x + 8 ).
Task 2: Describe two different types of inequalities(Which are not explained in course). Provide examples of each type of inequality and explain how to solve them.
Strict Inequalities
A strict inequality indicates a relationship where one expression is strictly less than ((<)) or strictly greater ((>)) than another, these inequalities exclude equality between expressions.
| Algebraic Example | (5x + 7 > 22) |
|---|---|
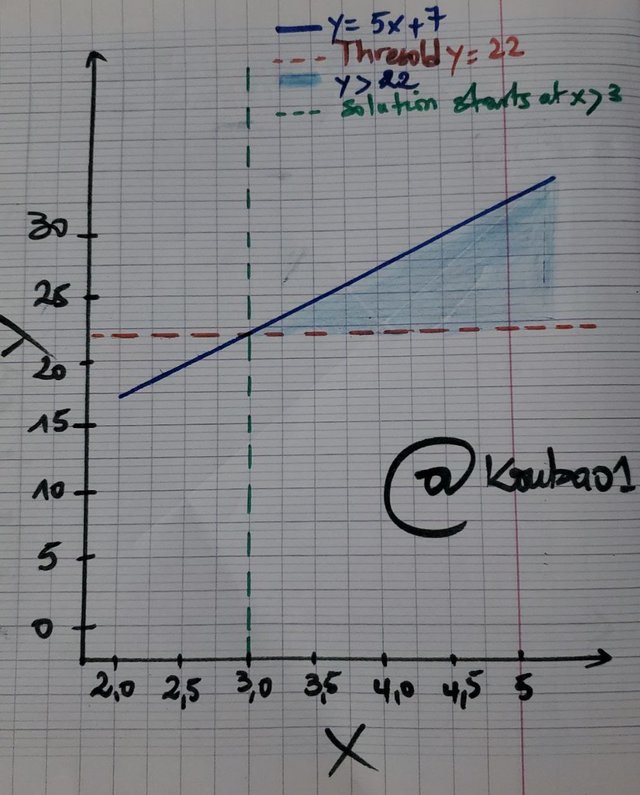
| Solving Steps | 1. Subtract (7) from both sides: (5x > 22 - 7) → (5x > 15). 2. Divide by (5): (x > 15/5) → (x > 3). |
| Result | The solution is (x > 3). |
Practical example:
A water park accepts visitors weighing more than (40 , \text{kg}) to use a water slide, if a person weighs (5x + 7) kg, from what value of (x) Can she use the slide?
The inequality (5x + 7 > 40) makes it possible to find that (x > 3), so the person must weigh a minimum of (3) additional units to be eligible.
Graphical representation:
This inequality is represented by a straight line ((y = 5x + 7)) and a region above this line for (x > 3).
Rational inequalities
A rational inequality involves fractions where the variables are present in the numerator, the denominator, or both.
| Algebraic example | ((2x−1)/(x+3))≤0 |
|---|---|
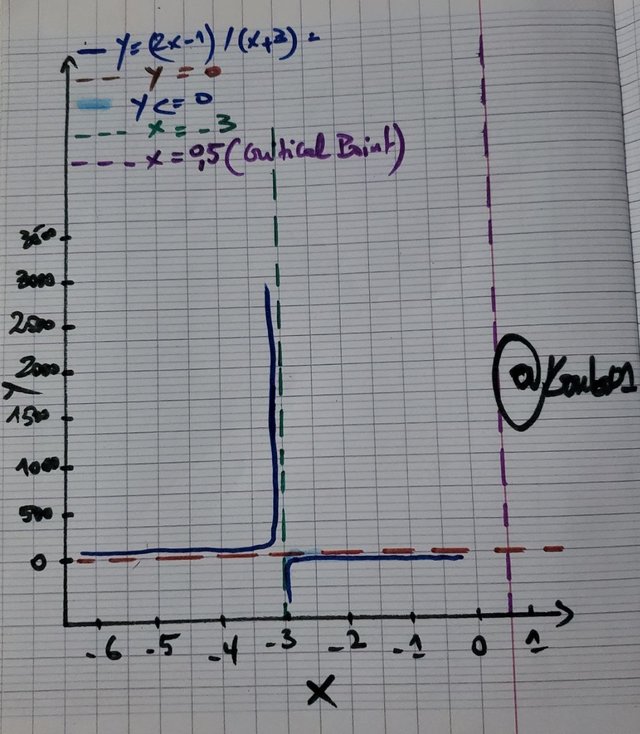
| Solving Steps | 1. Identify the critical values: 2x−1=0⟹x= 1/2 , 𝑥+3=0⟹𝑥=−3 2. Divide the (x) axis into intervals: (−∞,−3), (−3,1/2), (1/2,+∞) 3. Testing the intervals: The inequality is satisfied for x∈(−3, 1/2 ]. |
| Result | The solution is x∈(−3, 1/2 ] |
Practical example:
Suppose a company offers discounts if the ratio of sales ((2x - 1)) to the number of units produced ((x + 3)) is less than or equal to (0), The inequality ((2x−1)/(x+3))≤0 helps determine in which production range the company offers discounts.
Graphical representation:
Graphically, this inequality is represented by a fractional curve, with a region located under the (x) axis between the critical values (-3) and (1/2).
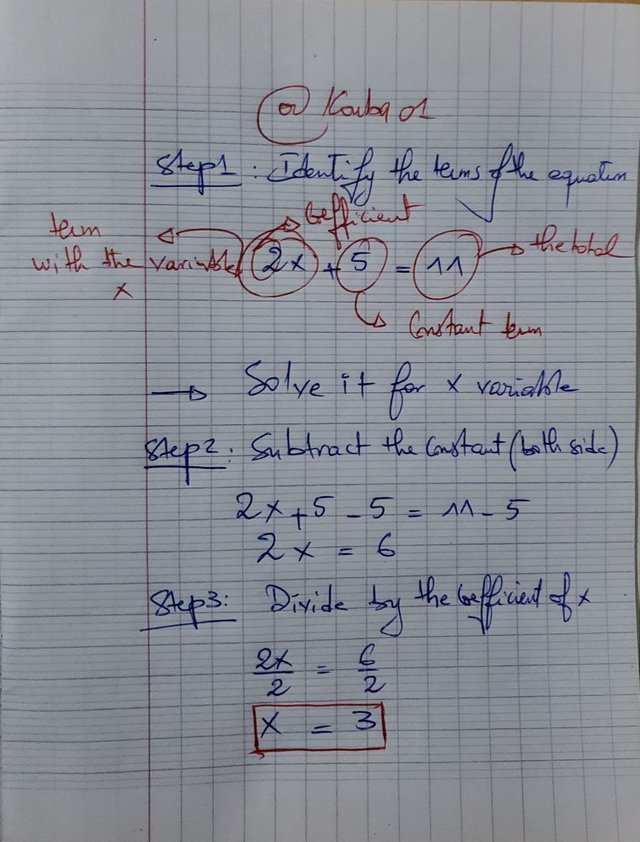
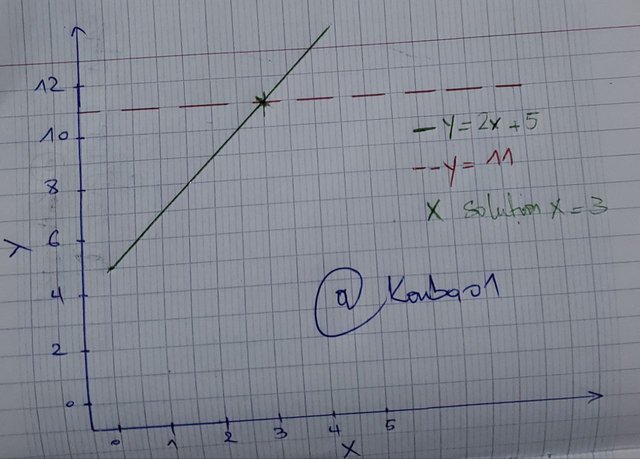
Task 3: Solve the following linear equation: 2x + 5 = 11.Show step-by-step solution and share its practical example of how this equation can be applied in real life scenario.
Practical Example: Real-life Application
Imagine a person has (11 $) and spends (5 $) on a meal. They use the remaining amount to buy two drinks of equal cost. How much does one drink cost?
The total cost is represented by the equation (2x + 5 = 11), where (x) is the price of one drink, (2x) is the total cost of the two drinks, (5) is the amount spent on the meal, and (11) is the total amount of money available. Following the steps above, we find (x = 3). Each drink costs (3 $).
Graphical Representation
The equation (2x + 5 = 11) is represented graphically as a straight line. The solution (x = 3) corresponds to the point where (y = 11), showing that the equation is balanced.
Task 4: Scenario: Tom's Bakery
Tom's Bakery is the most famous bakery of two and it's famous for its yummiest pastries and bread. Tom the owner wants to make sure that he has sufficient ingredients to meet the needs of his famous chocolate cake and chocolate cake recipe 2 cups of flour, 1 cup of sugar, and 1/2 cup of cocoa powder for each cake.
Solving Equation: Maximum Number of Cakes
Each ingredient places a constraint on the number of cakes Tom can bake.
For flour, each cake requires 2 cups, if Tom decides to prepare (x) cakes, the inequality becomes 2x≤10, dividing this equation by 2 gives x≤5, meaning flour limits Tom to a maximum of 5 cakes.
When it comes to sugar, each cake requires 1 cup, this gives us the inequality 𝑥≤8, which shows that sugar is enough to make up to 8 cakes.
For cocoa, each cake requires 0.5 cups, so the inequality becomes 0,5x≤4, dividing both sides by 0,5 gives 𝑥≤8, indicating that the quantity of cocoa available also makes it possible to prepareup to 8 cakes.
So although the sugar and cocoa are enough to make up to 8 cakes, the flour is the limiting factor, this means that no matter how much the other ingredients are in excess, Tom cannot make more than 5 cakes because he does not have enough flour to exceed this limit.
Solving the inequality: Prepare at least 6 cakes
Tom wants to check if he can make at least 6 cakes using his ingredients, based on the sugar the inequality becomes x≤8 and x≥6, which can be combined into 6≤x≤8, this means that Tom can theoretically prepare between 6 and 8 cakes if all the ingredients are sufficient.
However, although sugar and cocoa allow you to prepare at least 6 cakes, flour remains a major constraint, since it limits Tom to (x = 5), therefore it is impossible for Tom to satisfy the condition prepare at least 6 cakes with the amount of ingredients currently available.
Task 4: Scenario: Number of gallons Ashley needs.
Suppose there's a person named Ashley who is planning a road trip from City A to City B. If I talk about distance between two cities then it's around 240 miles. Ashley's car fuel tank can hold 12 gallons Suppose that his car gets 20 miles for each gallon then how many gallons of gas may Ashley purchase if he already has 2 gallons in his tank and he wants to have a minimum of 1 gallon left over when he arrives at City B?
Ashley is planning a road trip between cities A and B, separated by a distance of 240 miles, her car's tank holds up to 12 gallons of fuel, and her car uses 1 gallon to travel 20 miles, the goal is to determine how many gallons Ashley must purchase to complete the trip, knowing that she already has 2 gallons in her tank and wants to arrive at her destination with a minimum of 1 gallon remaining.
To travel the total distance of 240 miles, Ashley must calculate the total amount of fuel needed, dividing the total distance by the number of miles traveled per gallon gives us 240/20=12, thus, the total amount of fuel needed to making the journey is 12 gallons.
Ashley already has 2 gallons in her tank and wishes to keep 1 gallon minimum when she arrives, this means that she must purchase a sufficient quantity of fuel to reach these 12 gallons necessary while respecting this constraint, we can model this by the inequality x+2≥12−1, where (x) represents the quantity of gallons to purchase, by simplifying, this inequality becomes x+2≥11, then x≥9 after subtracting 2 on two sides.
In conclusion, Ashley should purchase at least 9 gallons to complete her trip, while keeping 1 gallon in her tank when she arrives, this ensures she will have a total of (2 + 9 = 11) gallons, this which is enough to cover the distance of 240 miles while respecting its needs, this solution takes into account its constraints and optimizes the use of its fuel.
Thank you very much for reading, it's time to invite my friends @graceleon, @adrianagl, @karianaporras to participate in this contest.
Best Regards,
@kouba01

- Equations and inequalities are connected to each other. You have explained the equations in a better way, equations are linear and quadratic, linear equations have one answer for every variable and quadratic have two same and different answers for 1 variable.
- You explained the question with more details, I have just used short sentences for explanation. Moreover, you have also provide the linear equation line and parabola curve for the quadratic equation.
- Solved the questions in a good way and I will say that medical student will learn and understand your topic easily.