SLC-S22W1/Variables and Expressions
.jpg)
Edited by Canva
Hello everyone and welcome to my participation post in this week's Algebra Challenge, organized by @khursheedanwar, thank you for this.
Algebra is a part of mathematics that handles symbols and the rules for manipulating them. These symbols or variables, represented usually by letters such as x, y, z, are used to represent numbers and/or quantities in equations and formulas. The primary goal of algebra is to solve these equations and understand the relation between variables.
Task 1
| Explain any two variables and expressions types other than that which are explained in this course. |
|---|
Some of these variables are Discrete Variables and Continuous Variables.
Discrete variables are a type of variables that can only have specific and distinct values, mostly used for counting and cannot be divided in small fractional values. For example, the number of red cars in a parking lot, this can be 3, 7, 20 but never 10.2 or a library can have 50, 64 or even 200 books but not 20.6. This means that a discrete variable if finite and can be numbered.
Continuous Variable is the opposite of a discrete one, meaning that it can take an infinite number of values in a range. It can include decimals and fractions. For example, the amount of liquid in a glass can be 250 ml but after drinking some it is 224,95 ml. We also use Continuous Variables for measuring the weight of a person, in the morning it can be 68.4 kg and in the evening 68.8 kg.
Expressions are a combination of variables, numbers and mathematical operations such as multiplication, division, exponents, and more. The key points about them is that they have no equal sign and can be evaluated if you know the values of the variables. There are a variety of expressions used in algebra, but some more interesting ones are Rational Expressions and Exponential Expressions.
Rational Expressions include fractions with polynomials in the numerator and/or denominator which cannot be 0. They can be used in practice to describe the time (t) it takes a vehicle to travel the distance (d) with at the speed (s). And so we can write the expression for t as : t = d/v . If d = x² +2x+1 and s = x - 3, the expression for t becomes: t = x² +2x+1/x - 3, where x cannot be 3.
Exponential Expressions involves a constant base that is raised to a variable exponent or a variable based raised to a constant exponent. For example: 2x ,x² ,(1.5)n. This type of expression can be used by banks to calculate the total amount (T.A) from a bank account after y years, when we know the initial amount (I.A) and the annual interest rate (r): T.A = I.A * (1+r)t. If the deposit 1000 $ and have a 3% annual interest rate for 4 years we get: T.A = 1000 * (1 + 0.03)4 => T.A = 1000 * (1.12550881). So after 4 years, we will have 1,125.50881 $ in the bank account.
Task 2
| Show how to evaluate an algebraic expression if the values of the variables are given. |
|---|
Let's consider that we have the expression E = 2x²y + 4xy² - 3y, where x = 3 and y = 2.
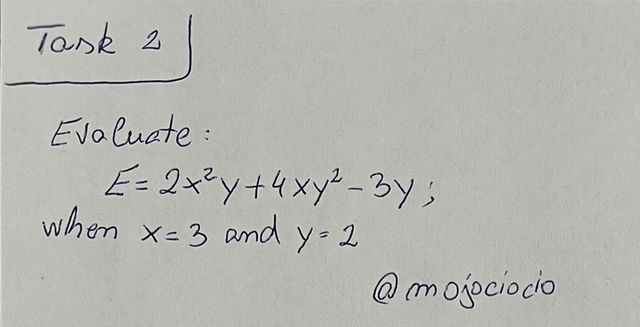
The values for x = 3 and y = 2 are substituted directly in the expression, which will give us E = 2(3)²(2) + 4(3)(2)² - 3(2). This represents an important step that allows us to transform our algebraic expression in a numerical one, that can be simplified.

Once we get our expression in a manageable, numeric form, we start by evaluating it and apply PEMDAS (Parenthesis, Exponents, Multiplication, Division, Addition, Subtraction) accordingly, from left to right. Since we don't have any parenthesis to do first, we can start with the exponents first: (3)² = 9 and (2)² = 4, by replacing them in the expression, we have: E = 2(9)(2) + 4(3)(4) - 3(2). At this point, there are no more powers that need to be calculated so we can do the multiplications.
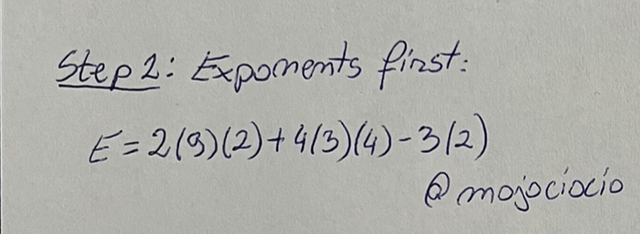
This is step is done in order, from left to right. First, 2 * 9 * 2 which gives us 36, 4 * 3 * 4 = 48 and lastly 3 * 2 = 6. These results are inserted into our expression which gives us E = 36 + 48 - 6.

We continue with Addition and Subtraction by adding the first 2 terms: 36 + 48 = 84, then we substract 6, giving us E = 78. The final result of our expression evaluation is 78.
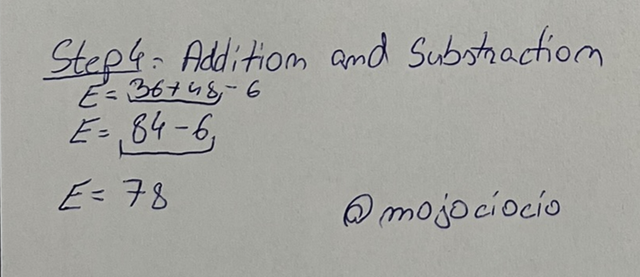
Task 3
| Simplify this expression: 3(2x - 1) + 2(x + 4) - 5 |
|---|

The first step in simplifying the given expression is to expand the parenthesis by using the distributive property: 3(2x - 1) becomes 6x - 3 and 2(x + 4) is 2x + 8. After this step, the expression becomes: 6x - 3 + 2x + 8 - 5, in which point we can combine like terms. The ones containing x gives us 6x + 2x = 8x, and the constants: -3 + 8 - 5 give us 0. The simplified expression is: E = 8x.
| Evaluate this expression: (x^2 + 2x - 3) / (x + 1) when x = 2 |
|---|

First step is to substitute x with 2 into our expression, giving us: E = 2^2 + 2(2) - 3/2 + 1. Next, we calculate the numerator N, by doing 2^2 = 4, followed by 2(2) = 4, thus having 4 + 4 - 3 = 5. Therefore, the numerator is 5. Calculating the denominator, 2 + 1, giving us 3. The expression becomes E = 5/3, which can be approximated to 1.67.
| Solve the following equation: 2x + 5 = 3(x - 2) + 1 |
|---|
First step in solving the given equation, is to look at the right side of it and distribute the term 3(x - 2), giving us 3x - 6, and after adding the 1, our equation is: 2x + 5 = 3x - 5. The second step implies to get the x-terms on a side and the constants on the other: 2x - 3x = -5 - 5. Simplifying it, we get -x = -10. Finally, we have to multiply both sides by -1, giving us x = 10.
Task 4
| Suppose there's a bakery selling a total of 250 loaves of bread per day. They are selling whole wheat and white bread loaves with numbers of whole wheat loaves sold being 30 more than the number of white bread loaves. If x is representing number of white bread loaves sold out and bakery is making a profit of $0.50 for each white bread loaf and $0.75 for each whole wheat loaf then please write an expression for representing bakery total daily profit. |
|---|
To solve the given problem and create the expression, we need to analyze the given information. We know that the number of white bread loaves that are sold is x and the number of whole wheat loaves is 30 more than the number of white ones, giving us whole wheat = x + 30. We are also being told that the profit made by the bakery on 1 white loaf is $0.50 and for 1 whole wheat, $0.75. The goal is to find the total daily profit expression. By adding all this information together we get:
x = number of white bread loaves
x + 30 = whole wheat loaves
Total Daily Profit = 0.5x + 0.75(x + 30)
By distributing 0.75 over the parenthesis, we get: 0.75x + 22.5 and the expression becomes: Total Daily Profit = 0.5x + 0.75x + 22.5. As a final step, we add the like x-terms and get that the total daily profit for the bakery is: Total Daily Profit = 1.25x + 22.5

| Suppose that cost of renting a car for a day is re-presented by the expression 2x + 15 and here x is the number of hours in which car is rented. If the rental company offers a package of 3x - 2 dollars for customers who take car at rent for more than 4 hours then write an expression for the total cost of renting the car for x hours and show how you simplify it. |
|---|
Similar to the previous scenario, to solve the problem and find the expression for the total cost of renting a car for x hours, we need to analyze the given data. You know that the cost of renting a car for one day is 2x + 15, where x = number of hours, but IF the rental period it greater than 4 hours, x > 4, they offer a package of 3x - 2 dollars.
So, the total cost can be written as the sum of the cost of renting for less than 4 hours + the cost of renting for more than 4 hours.
We get: Total amount = (2x + 15) + (3x - 2). Simplifying the expression by removing the parentheses, 2x + 15 + 3x -2, and combining like terms, the ones with x 2x + 3x = 5x, and the constants 15 -2 = 13, we get the total cost of: 5x + 13.

Thank you for reading and I'd like to extend an invitation to @ady-was-here, @radudangratian and @cmalescov to take part in this.
@tipu curate
;) Holisss...
--
This is a manual curation from the @tipU Curation Project.
Upvoted 👌 (Mana: 2/7) Get profit votes with @tipU :)
Look at you, pen and paper
Yep, felt like I was back in school