"SLC-S22W1/Variables and Expressions"

josepha (78)in #algebra-s22w1 • 2 days ago

canvas

Friends we are here again to learn in this SLC S22W1 which Variables and Expressions topic is what I have participated in here.

Explain any two variables and expression types other than those that are explained in this course. (Practical and algebraic examples are required!)

Here I will be explaining to you the two variables and expressions that were not discussed in the professor's post. Boolean and area (list) expression variables are the two variables and expression types I have explained in this post.

Boolean Variables and Expressions:

By definition, Boolean Variables are simply the type of variables that possibly hold two values such as; a true value or a false value. It is an expression that takes care of logical statements that are elevated based on conditions.

A good practical example, of Boolean Variables in Python programming languages, can be expressed as: is_adult = age >= 20

In the practical example, the boolean variable is is_adult. The expression age>=20 evaluates to true if age is 20 or more, otherwise it will evaluate false if age 20 is less.

Based on the algebraic example we can say;
Let;

x > 0 a condition
If x = 10 then
Boolean expression x > 0 evaluates to true.
If x = - 6 then
Boolean expression x > 0 evaluates to false

Array (List) Variables and Expressions

By definition, array (list) simply means a collection of variables stored in a single variable. In this type of variable, any expression that has to do with arrays operates on the entire array of elements.

A good practical example, of array (list) variables in Python programming languages can be expressed as shown below 👇.

numbers = [1, 2, 3, 4]
sum_numbers = sum(numbers)

In the practical example, numbers is an array variable, and the expression sum(numbers) is what computes the sum of all the elements, resulting in 10.

Based on the algebraic example we can say;

A = [a1, a2, a3] represent numbers of array.
This then means the operation will be sum (A) = a1+a2+a3.
If A = [2, 4, 6] then
Sum (A) = 2 + 4 + 6 = 12

Show your way of evaluating an algebraic expression if values of variables are given. Step-by-step explanation required! (The more you will be detailed and accurate, the more your task will be perfect!)

My ways of evaluating an algebraic expression are very easy I will be sharing with you all the step-by-step way of evaluating an algebraic expression if values of variables are given.

Expression to Evaluate

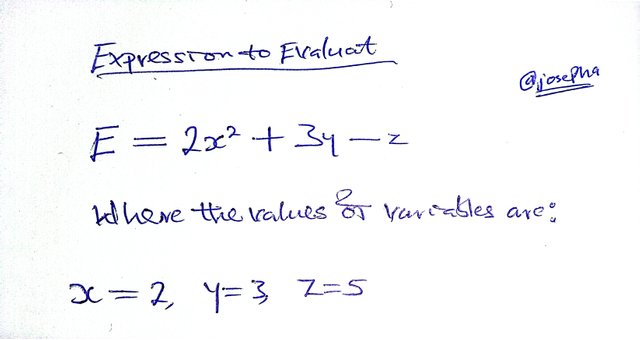
Looking at the above image where I have stated the expression, we have the following variables;

X = 2
Y = 3
Z = 5

The Step by Step Explanation required:

Step1: I will have to start with the given algebraic expression as;

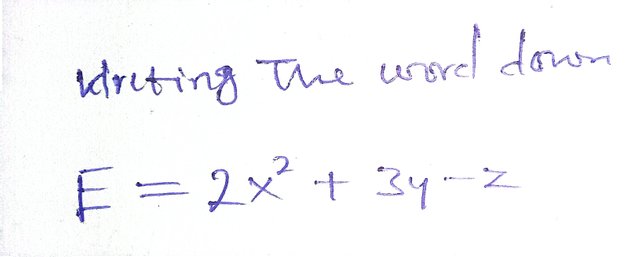
At this point, I have to write the word down on paper, because I don't know how to apply 2x raise to power 2 on the Steemit platform which I believe putting it on paper will help the audience (readers) to understand better.

Step 2: Substitution.
I will have to substitute the given values and replace each of the variables in the expression with its corresponding value which will then be expressed as shown below 👇.

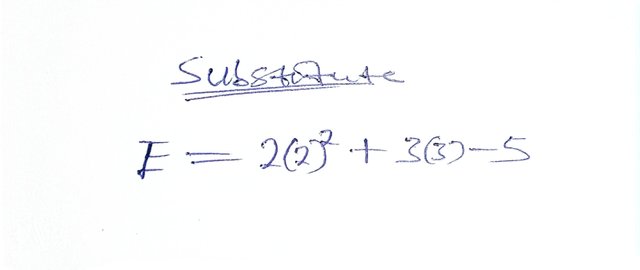
Step 3: Simplify. I will have to simplify the term involving the exponent 2 raised to the power 2

E = 2(4) + 3(3) - 5

Step 4: I will have to perform Multiplication by simplifying the terms.

E= 8 + 9 - 5

Step 5: I will have to perform both additions and substation
Add 8 + 9 = 17
17 - 5 = 12
E= 12

Task 3

• Simplify this expression: 3(2x - 1) + 2(x + 4) - 5

In this task, I applied two steps to solving the problem.
First I expand the term distribute the constraints into the parentheses and substitute it into an expression. The second thing I did was combine the like terms involving x and the constants which gave me a final answer as 8x

• Evaluate this expression: (x^2 + 2x - 3) / (x + 1) when x = 2

In this task, when you take a look at the problem solved in the paper you will see that I used three steps in solving the problem the first step was substituting x = 2 into the numerator, and x = 2 into the denominator x + 1 which I then applied division of 5/3 and arrived at 1.6

• Solve the following equation: 2x + 5 = 3(x - 2) + 1

In this task, I first expand the right-hand side and distribute the 3 into x - 2 before I then simplify the equation and finally solve for x and divide both sides by 1.

• Suppose there's a bakery selling a total of 250 loaves of bread per day. They are selling whole wheat and white bread loaves with the number of whole wheat loaves sold being 30 more than the number of white bread loaves. If x represents several white bread loaves sold out and the bakery is making a profit of $0.50 for each white bread loaf and $0.75 for each whole wheat loaf then please write an expression representing the bakery's total daily profit. • Suppose that the cost of renting a car for a day is represented by the expression 2x + 15 and here x is the number of hours in which the car is rented. If the rental company offers a package of 3x - 2 dollars for customers who take a car at rent for more than 4 hours then write an expression for the total cost of renting the car for x hours and show how you simplify it.

The expression for the bakery's total daily profit

Based on the question, x is = the number of white bread loves sold.
x + 30 is the number of whole wheat loaves of bread that are sold.
250 is the total loaves of bread sold per day.

x + (x + 30) = 250

Simplify;

2x + 30 = 250

2x = 220 implies x = 110

However, in the question

110 is = to the white bread loaves sold
110 + 30 = 140 is the whole wheat loves sold.

At this point, we will have to write the expression for profit as

Profit per white bread loaf	$0.50
Profit per whole wheat loaf	$0.75

Total profit = (0.50x) + (0.75(x + 30))

At this point, we will have to simplify the expression by substituting the values;

Total profit = 0.50x + 0.75x + 0.75(30)

Total profit = 1.25x + 22.5

Total Cost of Renting the Car:

Based on the given questions, we will have to first write the expression of the cost of renting the car for x hours which will be expressed as; 2x + 15