LeanAgent: The First Life-Long Learning Agent for Formal Theorem Proving in Lean, Proving 162 Theorems Previously Unproved by Humans Across 23 Diverse Lean Mathematics Repositories

Researchers from California Institute of Technology, Stanford, and University of Wisconsin, Madison introduce LeanAgent, a lifelong learning framework designed for formal theorem proving. LeanAgent addresses the limitations of existing LLMs by introducing a dynamic approach that continually builds upon and improves its knowledge base. Unlike static models, LeanAgent operates with a dynamic curriculum, progressively learning and adapting to increasingly complex mathematical tasks. The framework incorporates several key innovations, including curriculum learning to optimize the learning trajectory, a dynamic database to efficiently manage expanding mathematical knowledge, and a progressive training methodology designed to balance stability (retaining old knowledge) and plasticity (incorporating new knowledge). These features enable LeanAgent to continually generalize and improve its theorem-proving abilities, even in advanced mathematical domains such as abstract algebra and algebraic topology.

LeanAgent is structured around several key components that allow it to adapt continuously and effectively tackle complex mathematical problems. First, the curriculum learning strategy sorts mathematical repositories by difficulty, using theorems of varying complexity to build an effective learning sequence. This approach allows LeanAgent to start with foundational knowledge before progressing to more advanced topics. Second, a custom dynamic database is utilized to manage evolving knowledge, ensuring that previously learned information can be efficiently retrieved and reused. This database not only stores theorems and proofs but also keeps track of dependencies, enabling more efficient premise retrieval. Third, the progressive training of LeanAgent’s retriever ensures that new mathematical concepts are continuously integrated without overwriting previous learning. The retriever, initially based on ReProver, is incrementally trained with each new dataset for one additional epoch, striking a balance between learning new tasks and maintaining stability.

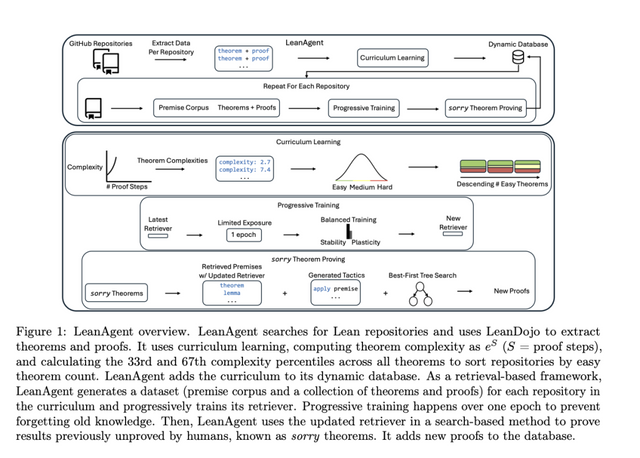
LeanAgent demonstrates remarkable progress compared to existing baselines. It successfully proved 162 previously unsolved theorems across 23 diverse Lean repositories, including challenging areas such as abstract algebra and algebraic topology. LeanAgent outperformed the static ReProver baseline by up to 11x, particularly excelling in proving previously unsolved ‘sorry theorems.’ The framework also excelled in lifelong learning metrics, effectively maintaining stability while enhancing backward transfer, wherein learning new tasks enhanced performance on prior ones. LeanAgent’s structured learning progression, beginning with fundamental concepts and advancing to intricate topics, showcases its capacity for continuous enhancement—a crucial advantage over existing models that struggle to remain relevant across diverse and evolving mathematical domains.

The conclusion drawn from this research highlights LeanAgent’s potential to transform formal theorem proving through its lifelong learning capabilities. By proving numerous complex theorems that were previously unsolved, LeanAgent has demonstrated the effectiveness of a curriculum-based, dynamic learning strategy in continuously expanding and improving a model’s knowledge base. The research emphasizes the importance of balancing stability and plasticity, which LeanAgent achieves through its progressive training methodology. Moving forward, LeanAgent sets a foundation for future exploration in using lifelong learning frameworks for formal mathematics, potentially paving the way for AI systems that can assist mathematicians across multiple domains in real time, while continuously expanding their understanding and capability.