Reinforcement Learning using Asynchronous Advantage Actor Critic
Reinforcement learning is an extremely exciting field that has pushed the boundaries of artificial intelligence. In my research, I stumbled upon an effective reinforcement learning method called Asynchronous Advantage Actor Critic (A3C) published by DeepMind. This algorithm beats the famous DQN by quite a margin and also seems to yield more stable results. I wanted to give a high level explanation in this post of how the algorithm works, hopefully inspiring more people to apply it in their projects. If you’re interested in the code, I implemented the algorithm using Tensorflow and Keras inspired by this Medium article. The library is compatible with OpenAI’s Gym API.
Actor Critic Models
Before we dive into the asynchronous part, I’d like to explain Actor-Critic (AC) learning models. In a reinforcement learning problem, an agent exists in some state s and tries to choose an action a to maximize its discounted future rewards.
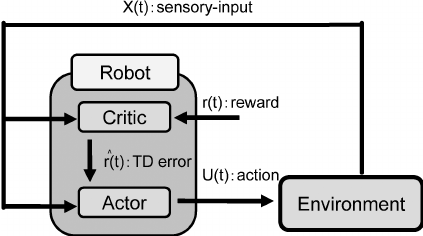
The AC agent is comprised of an actor and a critic. The actor attempts to learn a policy π(s) (AKA the rule that the agent follows) by receiving feedback from a critic. The critic learns a value function V(s) (the expected return in rewards), which is used to determine how advantageous it is to be in a particular state. The advantage is defined as A(s) = Q(s, a) - V(s). In practice, we don’t want to compute Q(s, a). Instead, we formulate an estimate of the advantage function as A(s) = r + γV(s’) - V(s), where r is the current reward and γ is the discount factor. This achieves the same result without needing to learn the Q function. An even more effective method would be to use generalized advantage estimation.
Objective Functions
Looking at the actor-critic agent from a neural network perspective, we would give the agent two outputs: value and policy. The value output predicts a scalar that learns the value function V(s). The policy output π(s) (softmax activation) is a vector that represents a probability distribution over the actions. We pick the action non-deterministically by sampling from this probability distribution. We denote π(a | s) as the probability of the sampled action a given state s.
We arrive at the following loss functions (we want to minimize these). R represents the discounted future reward (R = r + γV(s’)).
Value Loss: L = Σ(R - V(s))² (Sum Squared Error)
Policy Loss: L = -log(π(a | s)) * A(s)
But not so fast! While the loss functions above would work, it is better to introduce the entropy H(π) to the equation.
H(π) = - Σ(P(x) log(P(x))
Entropy is a measure of how spread out the probabilities are. The higher the entropy, the more similar each action’s probability will be, which makes the agent more uncertain about which action to choose. Entropy can be added to the loss function to encourage exploration by preventing the agent from being too decisive and converging at local optima
Policy Loss: L = - log(π(a | s)) * A(s) - β*H(π)
When we combine the two loss functions, we get the loss function for the model overall:
L = 0.5 * Σ(R — V(s))² - log(π(a | s)) * A(s) - β*H(π)
Notice that the loss for value is set to 50% to make policy learning faster than value learning. For more information on the derivations of these loss functions, I recommend watching David Silver’s RL lecture videos. With that, we can train our AC agent!
Asynchronous
The interesting part about A3C is the first A — asynchronous. DeepMind’s paper showed that by introducing asynchronous training, we can reduce the correlation between episodes, improving various methods of learning including Q-learning (better data efficiency). It is also a more efficient use of multi-core CPUs, allowing us to train agents to do quite amazing things with just a laptop.
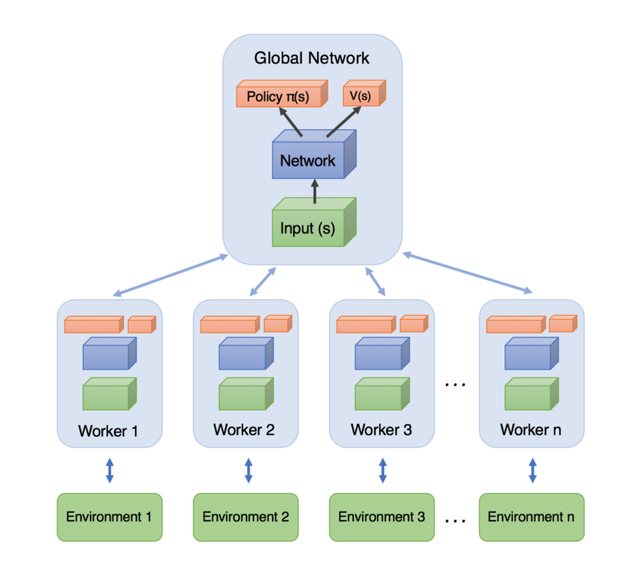
A3C works by spawning minion AC agents, each performing actions in their own separate environments and updating the master neural network after a certain amount of actions have been taken. The individual agents sync their weights with the master network after every gradient update.
However, more recent research from OpenAI suggests that A2C (without asynchronous learning) performs equally well when using GPUs. We can argue that the key benefit of A3C is that there are parallel agents learning at the same time, allowing a policy to be evaluated on multiple trajectories simultaneously.
That’s it for a high level overview of A3C. If you’re interested in checking out a detailed implementation of the algorithm, be sure to check out my Github repository.
I’ll be following up on this post shortly on how I applied A3C to a mobile game I developed called Relay . Feel free to leave me suggestions or ask questions in the comments section!
Congratulations @calclavia! You received a personal award!
Click here to view your Board
Congratulations @calclavia! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!