2-3 Rosenblatt의 퍼셉트론 알고리듬을 Processing으로 코딩하자!-I
Rosenblatt의 퍼셉트론 알고리듬에서 입력 벡터 코딩에 대해서 알아보자. 20X20 Photocell 센서를 사용하면 WeMos LOLIN 조도센서 실험에서처럼 빛의 입력에 따라 조도센서 소자의 저항 값이 변동되며 흐르는 전류 값도 변동된다. 예를 들면 햇빛이 강렬할 경우 100Ω 아래로 내려가기도 하며 한편 깜깜할 정도로 어두울 경우 40KΩ 까지 저항 값이 커지기도 한다.
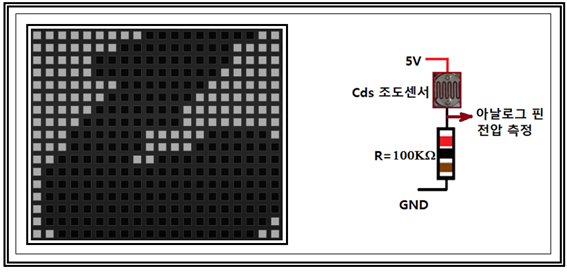
그림과같이 이미지센서 보드에 명암이 있는 이미지가 투사되면 각각의 조도센서가 반응하여 전압과 전류 변동이 발생한다. 지금은 아두이노 우노보드에서 아날로그 핀으로 전압 값을 읽으면 되는 간단한 작업이지만 Rosenblatt 시대에 무려 400개 달하는 입력 전압을 체크하기가 쉽지 않았으리라.
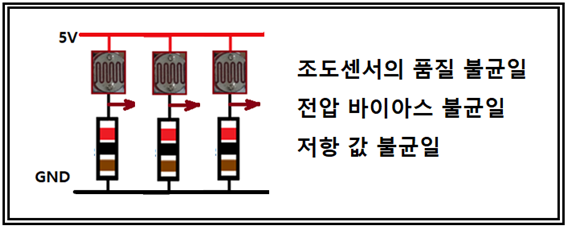
특히 조도센서와 저항을 직렬 연결한 400개의 이미지 센서를 설치하고 빛을 쪼여 줄 경우에 각 부품들의 불균일성으로 인해 측정되는 전압 값도 상당히 불균일 할 수 있다. 그래도 완전히 깜깜한 경우 조도센서의 저항 값이 40KΩ에 달하기 때문에 직렬 연결된 1KΩ 저항을 감안하여 측정하는 전압이 사실 0.0V 가되면 바람직하지만 5V/41=0.125V가 되는데 이처럼 0점에서 떨어진 값의 크기를 바이아스라고 하며 그나마 바이아스 값이 조도센서 별로 일정하지 못하고 등락도 클 수밖에 없다. 아울러 빛의 밝기가 점차 세어짐에 따라 측정 전압 값이 선형적으로 비례하면 바람직스럽다. 머신 러닝에서 선형회귀법을 사용하는 경우에 기울기를 나타내는 웨이트와 바이아스 항이 항상 나타나는데 위 조도센서 사례에서 바이아스의 현실적인 사례가 될 것이다.
퍼셉트론 코딩과정에서도 마찬가지로 Rosenblatt 이나 MNIST 문제에서는 이미지 센서 측정에서 측정된 전압에 따라 흑백 명암 값이 0∼256 범위로 얻어질 수 있으며 256으로 나누어 normalization 하면 0∼1.0 사이의 값이 얻어진다. 만약 컴퓨터 코드에서 알고리듬만 가지고 작업할 경우 Random 한 입력 데이터를 400개 생성하기는 어렵지 않다. 애를 들어 x = random(1) 이란 명령을 실행하면 x 값은 항상 0∼1 사이의 실수 값이며 음의 값도 필요하다면 x =random(-1, 1)과 같이 범위를 부여 하면 된다.
하지만 어차피 컴퓨터 코드의 알고리듬이란 것은 입력이 1개, 2개, 3개 일 때도 실행이 되어야 하고 400개는 물론 784개일 때도 실행이 되어야 한다. 그러므로 아주 간단하게 이미지로서 현실적인 감은 떨어지겠지만 첫 단계에서는 2개짜리 입력을 생각해 보도록 하자.
Programming 툴로서 C/C++ 언어를 사용하는 Java 모드의 Processing을 사용하기로 한다. 아두이노 IDE처럼 무료 다운이 가능하며 사용구조가 setup과 loop 대신 draw를 사용하는 아두이노 스타일인데 그래픽이 지원이 뛰어나다. Processing IDE는 www.processing.org에서 무료로 다운 받을 수 있다.
퍼셉트론 코딩에서는 draw에서 무한 반복할 것은 아니므로 setup에서 입력 데이터 inputs를 다음과 같이 배열(array)을 사용 한줄 처리하기로 하자. 즉 이는 터무니없게 조도센서 2점으로 이미지를 센싱하도록 ㅋㅋㅋ 수준의 퍼셉트론을 꾸몄다는 얘기다. 간단한 수치 예제를 하기 전에 주의할 점을 짚어 보자. Rosenblatt의 퍼셉트론은 입력 값이 1개씩이며 N개의 센서가 있는 문제다.
하지만 여기서 이하 다루는 예제는 2차원 예제로서 아래와 같이 x 와 y 좌표로 표현되며 좌표 세트 개수는 정하면 된다. 또 주의할 점은 이 예제에서의 y는 Rosenblatt의 라벨 값에 해당하는 yi 와는 다르다는 점에 유의하자.
∙∙∙
float[] inputs = {-1, 0.5};
∙∙∙
웨이트를 준비해야 하는데 Rosenblatt의 방식은 좀 더 고려를 해봐야 할 필요가 있다. 따라서 가장 쉽게 해 볼 수 있는 방법은 Random number로 처리하는 것이다. 입력이 2개이므로 웨이트도 2개만 준비하자. 아울러 이 부분은 Perceptron 이란 명칭으로 class 처리를 하여 메인 프로그램에 해당하는 setup에서 불러 쓸 예정이다.
∙∙∙
float[] weights = new float[2];
∙∙∙
현재 웨이트는 weights 라는 2개짜리 배열 오브젝트로 정의 된다.
다음의 코드 내용은 class 내부에서 weights.length 명령에 의해서 그 값이 2이므로 인덱스 i 의 범위를 정해 주고 random(-1, 1) 명령 사용에 의해 -1과 +1 사이에서 실수형태의 random 수를 생성한다. 이 부분은 처음에 0의 값을 부여하고 다음 번 웨이트를 계산하는 벡터 공식을 제안하였던 Rosenblatt의 알고리듬과 현재로서는 일치하지 않는 부분이지만 웨이트 벡터 업데이트가 먼저 이루어지게 되면 Rosenblatt의 코드와 마찬가지로 코드 실행에 아무런 문제가 없게 된다.
∙∙∙
//Constructor
Perceptron() {
//initiallize the weights randomly
for ( int i = 0; i < weights.length; i++) {
weights[i] = random(-1, 1);
}
∙∙∙
Rosenblatt은 그의 알고리듬에서 N개로 구성되는 입력 값과 아울러 곱하기 작업을 할 웨이트 값을 벡터량으로 간주하여 내적 연산을 실행하며 다음과 같이 시그마에 의해 합산 작업을 하였다.
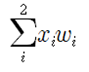
Rosenblatt의 퍼셉트론은 N이 400 이므로 웨이트도 400개가 되어야 한다. 하지만 우리가 작성하는 2개 입력 문제에서는 웨이트도 2개면 된다.
그 다음 단계에서는 합산 결과가 0보다 큰지 작은지를 판단하여 0보다 크면 +1을 아니면 –1을 부여한다. 이 부분이 Rossenblatt의 알고리듬에서 sign함수에 의한 판정 부분인데 신경망으로 치면 Activation 조건에 해당한다. 시그마에 의한 합산 결과 실수 값 n이 sign 함수에 입력되면 판정하여 라벨 값 +1 이나 –1을 돌려준다.
//The activation function
int sign(float n) {
if (n >= 0) {
return 1;
}
else {
return -1;
}
}
입력 벡터 inputs를 받아 random 명령으로 생성한 웨이트 값을 사용해 시그마에 의한 합산과정을 거친 후 sign 함수를 불러 라벨 값을 계산해 내는 class 내에 포함되어 있는 루틴 guess는 다음과 같다.
∙∙∙
int guess(float[] inputs) {
float sum = 0;
for ( int i = 0; i < weights.length; i++) {
sum += inputs[i]*weights[i];
}
int output = sign(sum);
return output;
}
∙∙∙
이로서 간단하지만 2개짜리 입력 벡터 데이터를 준 상황에서 random 한 웨이트를 사용하여 라벨 값을 계산하는 루틴이 완성되었다.
setup에서 입력 데이터 inputs를 설정하는 내용을 제외한 여기까지의 내용전부를 class Perceptron {∙∙∙} 으로 처리하고 헤더영역과 setup을 완성해 보도록 하자.
brain 이라는 이름으로 Perceptron class를 선언하고 setup에서 그래픽 화면을 임의로 size(200,200)으로 설정한다. class 선언된 Perceptron을 new 오브젝트 brain으로 설정한다. 입력 벡터 inputs를 만들어 주고 brain,guess에 입력해 준 후 돌아오는 최종 출력을 guess 로 두어 콘솔창에 출력하자. 현재 무한 반복해야할 루틴의 필요성이 없으므로 draw()는 비워둔다.
Perceptron brain;
void setup() {
size(200,200);
brain = new Perceptron();
float[] inputs = {-1, 0.5};
int guess = brain.guess(inputs);
println(guess);
}
void draw() {
}
이 루틴을 실행해 보면 “+1” 이나 “-1”이 나옴을 확인할 수 있다. 정확하게 교대로 “+1” 과나 “-1”이 출력되는 것이 아니고 여러번 해보면 통계적으로는 50:50임을 알 수 있다.

이 코드를 한번 실행하면 random 명령을 사용하여 생성한 웨이트 벡터가 한번 사용되고 끝나지만 차 후 업데이트할 코드에서는 초기 값을 한번 생성 후 학습에 따라 지속적으로 업데이트를 통해 웨이트 벡터가 갱신 될 것이다.
다음 편에서도 이어서 이 기본적인 코드를 토대로 업데이트하여 퍼셉트론 코드를 편집해 나갈 것이다.
//Simple_perceptron_01
//The activation function
int sign(float n) {
if (n >= 0) {
return 1;
}
else {
return -1;
}
}
class Perceptron {
float[] weights = new float[2];
//Constructor
Perceptron() {
//initiallize the weights randomly
for ( int i = 0; i < weights.length; i++) {
weights[i] = random(-1, 1);
}
}
int guess(float[] inputs) {
float sum = 0;
for ( int i = 0; i < weights.length; i++) {
sum += inputs[i]*weights[i];
}
int output = sign(sum);
return output;
}
}
Perceptron brain;
void setup() {
size(400,400);
brain = new Perceptron();
float[] inputs = {-1, 0.5};
int guess = brain.guess(inputs);
println(guess);
}
void draw() {
}
날이 너무 덥습니다......덥다 ㅠ
잘 읽었습니다. 오늘도 좋은 하루 보내세요~~!
내일 업데이트해서 그래픽으로 뭔가 볼 수 있도록 Processing.org에서 한번 클릭해서 다운받으세요.
pairplay 가 kr-dev 컨텐츠를 응원합니다! :)