21-02-2025 - Education - Linear Algebra - Projective Extension [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

[ENGLISH]
21-02-2025 - Education - Linear Algebra - Projective Extension [EN]-[IT]
With this post I would like to provide some brief notions about the technical topic mentioned in the subject.
The context in which we operate is that of analytical geometry or linear algebra
(code notes: MOD-60)

Projective Extension
The projective extension of an affine transformation is a way to represent the transformation in a projective space, which includes an additional dimension.
This allows us to deal with points at infinity and to unify affine and projective transformations in a single mathematical structure.
Basically, if we have an affine transformation in a two-dimensional space (2D), we can extend it to a three-dimensional space (3D) simply by adding a homogeneous coordinate.

Technical definition
Below is the technical definition of what projective transformations are.
Let's go...
Consider n-dimensional projective space

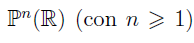
Is...

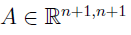
...an invertible matrix.

The application...

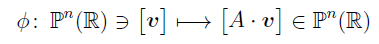
... is called projective transformation.

Matrix A is denoted by

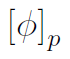
Exercise
Let's try the following exercise
Given the affine application...

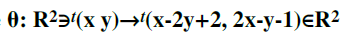
... and always denoted by θ its projective extension which of the following is [θ]p?

First of all, below I indicate the meaning of some symbols:

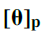
This indicates the matrix of the projective transformation θ

∈ = membership of an element to a set.

∋ = the inverse symbol of ∈ indicates that a set contains an element.

Exercise solution
To find the matrix of the projective transformation θ, we must consider the extension of the given affine transformation.
The affine transformation θ is defined as.

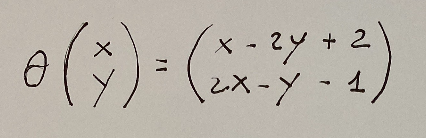
To extend the transformation in the projective case we need to add a third coordinate. This third coordinate must be homogeneous.
So we add a third z coordinate and write the transformation in matrix form.
The extended form will then be the following:

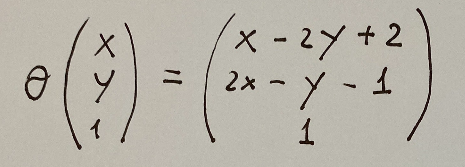
At this point what we need to do is describe what is written above as a matrix multiplication. We will get the following

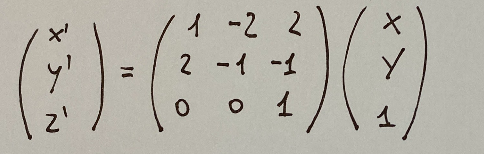
At this point we will have that the matrix of the projective transformation θ will be like the matrix written below:

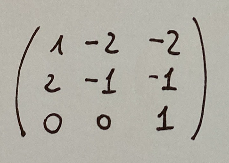
The correct solution is the next

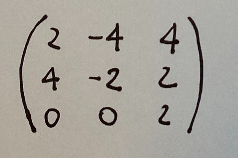
The one above is a matrix equivalent to our found matrix, multiplied by 2.

Conclusions
The projective extension is useful because it simplifies the treatment of complex geometric transformations and allows you to work with points at infinity in a natural way.
Projective extensions allow: the unification of transformations, the incorporation of points at infinity, they can be represented by a matrix.

Question
Have you ever heard of projective transformations? Did you know that, in cartography, projective transformations are useful for projecting the curved surface of the Earth onto flat maps, maintaining the proportions and relative distances?

---

---

[ITALIAN]
21-02-2025 - Education - Algebra lineare - Estensione proiettiva [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello della geometria analitica o algebra lineare
(code notes: MOD-60)

Estensione proiettiva
L'estensione proiettiva di una trasformazione affine è un modo per rappresentare la trasformazione in uno spazio proiettivo, che include una dimensione aggiuntiva.
Questo permette di trattare punti all'infinito e di unificare le trasformazioni affini e proiettive in un'unica struttura matematica.
Sostanzialmente se abbiamo una una trasformazione affine in uno spazio bidimensionale (2D), possiamo estenderla ad uno spazio tridimensionale (3D) semplicemente aggiungendo una coordinata omogenea.

Definizione tecnica
Qui di seguito è riportata la definizione tecnica di cosa sono le trasformazioni proiettive.
Partiamo...
Si consideri lo spazio proiettivo n-dimensionale

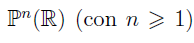
Sia...

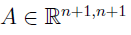
... una matrice invertibile.

L’applicazione...

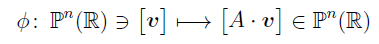
... è detta trasformazione proiettiva.

La matrice A è indicata con

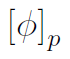
Esercizio
Proviamo ad eseguire il seguente esercizio
Data l'applicazione affine...

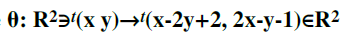
... e indicata sempre con θ la sua estensione proiettiva quale delle seguenti è [θ]p?

Prima di tutto qui di seguito indico il significato di alcune simbologie:

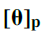
Questa indica la matrice della trasformazione proiettiva θ

∈ = appartenenza di un elemento a un insieme.

∋ = il simbolo inverso di ∈ indica che un insieme contiene un elemento.

Svolgimento esercizio
Per trovare la matrice della trasformazione proiettiva θ, dobbiamo considerare l'estensione della trasformazione affine data.
La trasformazione affine θ è definita come.

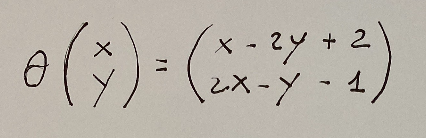
Per estendere la trasformazione nel caso proiettivo dobbiamo aggiungere una terza coordinata. Questa terza coordinata dovrà essere omogenea.
Quindi aggiungiamo una terza coordinata z e scriviamo la trasformazione in forma matriciale.
La forma estesa sarà quindi la seguente:

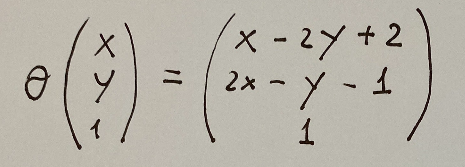
A questo punto quello che dobbiamo fare è descrivere quanto scritto qui sopra come una moltiplicazioni di matrici. Otterremo quanto segue

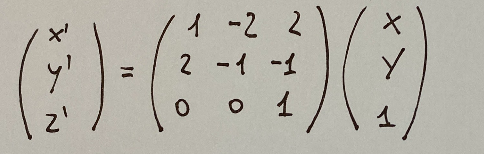
A questo punto avremo che la matrice della trasformazione proiettiva θ sarà come la matrice scritta qui sotto:

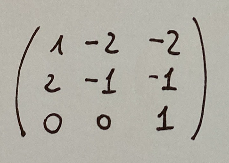
La soluzione corretta è la seguente

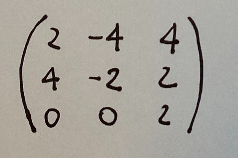
Questa qui sopra riportata è una matrice equivalente alla nostra matrice trovata, moltiplicata per 2.

Conclusioni
L'estensione proiettiva è utile perché semplifica il trattamento delle trasformazioni geometriche complesse e permette di lavorare con punti all'infinito in modo naturale.
Le estensioni proiettivi permettono: l'unificazione delle trasformazioni, l'incorporazione dei punti all'infinito, esse possono essere rappresentate mediante matrice.

Domanda
Avete mai sentito parlare di trasformazioni proiettive? Lo sapevate che, in cartografia, le trasformazioni proiettive, sono utili per proiettare la superficie curva della Terra su mappe piane, mantenendo le proporzioni e le distanze relative?

THE END