1.前言
如果回归方程为线性函数,则优化推断很容易形成。因此,线性模型的使用率很高,甚至成为首选。以为撒大网就能捉到大鱼,结果可能捉不到鱼。因为大多数实践课题不是线性的。如果处理不当,会掉入线性陷阱。
使用线性模型是有条件的。除非确有把握,否则,在试验设计时,线性只是一种假设,必须加以检验。如果检验结果,过程不是线性的,必须采取补救措施,修正模型,从而也修正实验设计,重估参数。
非线性过程使用线性模型,其回归系数估计值不是主效应估计,而是多重效应的叠加混杂,离真正的主效应相差太多。推断的优化方向与应该的优化方向有一个很大的夹角,这个夹角依赖于主效应估计与其实际值的差异。因而可能不代表优化方向,甚至背道而驰。
根据数学分析原理,在小范围内,曲面可以用平面来近似,它预报的优化方向与实际优化方向的偏差较小。
这种方法既可以避开研究交互效应,试验数目少,优化速度快,效果好。
2. 方法描述
一项产品的性能 y (假定 y 越多越好)受一些变量(因子)x
1,x
2,...,x
p的影响。
我们可以假设它们之间存在一种关系
y=f(x1,x2,...,xp)+e ------(1),
这里 f(X) 是某个函数,e 是误差。
函数 f 是什么形式,实验之前不清楚。我们常常使用 线性的或非线性的这样的数学术语来粗略地表述这种关系。
所谓非线性关系,是指随着 x
i 的变化,y 的变化不是直线关系。只有一个变量时是曲线,两个变量时是曲面,
在多变量情况下,画不出图来,称为超曲面。数学表达式多种多样,这里不详述。
所谓线性关系,是指随着 x
i 的增加,y 呈直线上升或下降。直线是相对于一个变量而言,两个变量就是平面。
更多的变量,在多维空间中,画不出图来,称为超平面。用数学式表示,
y=f(X)=b0 +b1 x1 + b2x2+ ...+ bpxp+e ------(2),
线性预报函数很容易推断出优化方向。
假定 y 是越大越好,那么,如果第 i 个回归系数 b
i>0, 则 x
i越大越有利于 y,反则反之。
优化方案很容易形成。
正是非线性过程中响应变量与自变量之间的关系非常复杂,使用回归分析研究这种关系有些困难。
既然是非线性的,一定存在最大值点和最小值点。
一个曲面的最大值最小值在什么位置,事前不清楚,需要用试验来搜索。这就有搜索策略问题。
通常是大范围搜索。所谓撒大网捉大鱼的策略。
理论上,如果鱼存在,一定在大网里。鱼多大?网该织多密?太疏,鱼漏网。太密,则试验数太多,我们不能接受。
例如,5 个因子,每个因子 5 个水平(级别),总共有 5
5=3125个实验。
这个数目很难被接受。5 水平的密度还不够精密,10水平的试验数是 100,000。10 水平有时也不算精密。
许多工程师选择二水平正交表。用 8 个实验来实施这一捕鱼行动。
每个变量只有两个水平,两个因子相互配合只有四个试验点,拟合结果是一个平面。
就是说,我们已经假定了我们研究的过程是线性的(超平面)。
即,事实上是用一个平面去近似那个曲面。
平面的优化点一定在所研究区域的边界上。而峰点通常在所研究区域的内部。我们推断的优化点指向了相反的方向。
专业试验工作者会采取某些措施来弥补,经验不够时就会茫然失措,失去信心。这样的例子屡见不鲜。
为了形象地解释这一问题,我们举单变量的例子。
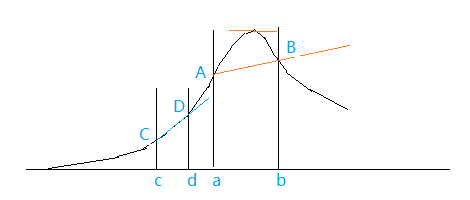
图1. 非线性过程示意图
假设 y 只依赖于一个变量,是非线性关系。最大点在什么位置,我们不清楚。
假如用 a,b 两点做试验,得到了直线AB,
这条直线的优化方向指向峰的一侧,那里是“山谷”,越往外推,距离峰越远。
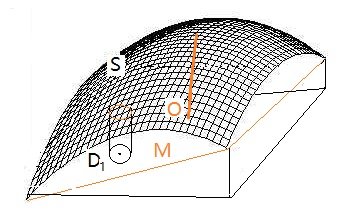
图 2 模拟二变量的情况,曲面 S 代表一个二元过程的本来曲面,它的最大值(优化点)是那条红色竖线,位置在点 O。
四个点拟合得到平面 M。那么,我们推断最大值点在右上方。外延出去越远,离真正的优化点 O 越远。
图2. 平面拟合曲面示意图
假如换一种策略。在一个小的局域中试验,在这个小的局域中,曲线可以用直线来近似,曲面可以用平面来近似。
由它导出的优化方向指向偏差不大。例如,图 1 中选择 c,d 两点,回归直线。
外延指向峰顶,经过几步外推会到达峰附近。由图 1 可见,一旦到底峰顶,该因子的效应估计值接近于0, 对参数的扰动很敏感。
图 2 中的小区域 D
1,它对应的小片曲面用平面来近似,外延指向峰顶,经过几步外推会到达峰附近。
在小局部范围内试验,用线性模型研究非线性过程比较好。
方法步骤如下:
- 选定一组观察变量, (x1, x2,...,xp),
从本专业知识出发,确定每个变量的变化区间,构成试验范围 D
- 在实验范围 D 内确定试验的起点 X0= (x01, x02,...,x0p) ,
建议该点在 D 的中部。以 X0 为中心,给每个变量 xi 确定一个小的变化范围。
建议单边 di 不超过该变量变化范围的10%。
- 选一个正交表,安排一组试验。建议采用不规则正交表,据情选用正交超立方或固定水平或混合水平。
- 完成试验后,用向后逐步回归分析,估计模型 (2) 的回归系数b'i(i=1,2,...,p)(作为bi的估计值)。
得到回归方程
y^=f(X)=b'0 + b'1 x1 + b'2x2 + ...+ b'pxp ------(3),
- 推断得到一个优化方案 X1= (x11, x12,...,x1p) 。原则如下:
如果b'i>0, 则 xi 往前进一个距离到 x1i=x0i+di ;
如果b'i<0, 则 xi 向后退一个距离到 x1i=x0i - di ;
如果b'i=0, 则遵循“价格贵的尝试少用,价格便宜的尝试多用。”的原则 前进一个距离或者后退一个距离。
- 用X1作试验点检验推断的优化效果,试验至少重复两次,作统计检验。比较试验结果。
如果效果好,继续推进。直到推断与验证严重不符,意味着已经到达峰点附近,可能跨越了峰顶,停止推进。进入下一步,修改方向,调整精度。
- 可以回到第 1 步,调整系统,重复操作;也可以不调整系统,只将试验区域移动到一个新点。
也可以把试验数据合并,回到第四步重估回归系数,重复其后步骤。
直到能够确认每个变量到达其稳定点 附近或者达到了理想的效果,即,回归系数估计值的绝对值都很小时,结束试验。
2. 说明与讨论
-
di不能太大,如果太大,可能超出平面近似曲面的允许范围;也不能太小,如果太小,信息差异可能比试验误差还小,被淹没不能被检出。
di究应该取多大?目前给不出标准。如果因子 xi 很敏感,就应该取小一点;否则可以大一点。
在试验过程中, di可以调整。
- 传统的正交表有局限性,特别是二水平表,试验点密度低,信息存在混杂叠加现象。而多水平表的列数少,试验数多,理论上信息也是混杂叠加的。
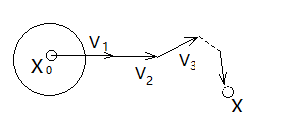
- 过程中试验点(区域)逐步移动,移向优化点。优化点实际上是一个区域,精度由 di确定。参见图 2.
图2. 一步一步地移动试验区域
- 步骤 5 的所谓前进一个距离或者后退一个距离的“距离”不一定恰好是 d 甚至可以是几个 d. 这需要试验者自己判断。
- 这种方法类似于梯度法。不同的是,梯度法不要求实验区域是小范围,梯度向量是对目标函数取偏导数的结果,如果目标函数是非线性的,不能只取主效应估计。有些作者采用二水平正交表,而不对交互项取偏导数,梯度向量就必然存在很大的误差。本方法采用线性模型,在小范围内试验,不存在取偏导数的问题。
Congratulations @shenzehe! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOP