SLC S22W3//Equations and Systems of equations
Hi Friends
I am Muhammad Ahmad and I hope you all will be fine and enjoying your lives. Today I am going to participate in the Third week of the Engagement Learning Challenge which our Dear, Instructor Mr. @khursheedanwar organized. First, l would like to thank him for organizing such a great lecture. By the way in this Lecture, we are gonna learn about equations like what is equations and the system of equations. So without wasting any time let's get into it.
Explain difference between linear and non linear systems of equations. Provide examples of each type of system of equation and describe their general forms. |
|---|
Linear Equations:
Those equations in which the variable's power is one are known as **Linear Equation.
Example 1:
x-1 = 0
Here in this example, we can see that the variable (x) has the power of 1. So it simply means that it is a Linear Equation.Example 2:
x/3-4 = 5
Here this example is also an example of Linear because here the power of x (variable) is 1.General Form:
Ax + By + C = 0
Non-Linear Equations:
Those equations in which the variable's power exceeds one are known as **Non-Linear Equation.
Example :1
x²-2 = 0
Here in this example, we can see that the variable (x) power is 2 as it exceeds 1 which simply means that this is a Non-Linear Equation.Example 2:
x3/6+8 = 2
Here's the example of Non-linear because here we can see that the Pwer of x is 3 which means that it is Non-linear.
- General Form:
ax2 + by2 = c
Describe any one method for solving system of linear equations and share atleast one step by step algebric example. |
|---|
So here we have to solve the linear equation but other than Substitution, elimination or graphing method the other method which I learned the previous year in GGrade 9 in my School Forward Public School Ring Road Peshawar here in the last exercises of Chapter 1 I have learned about that method very well and luckily that question was also come in my Board Papers, as this is very important Topic to learn. Basically Matrix method is a systematic way of solving Linear equations.
Solving the following Linear Equation by Matrix Method.
x + y = 5
x − y = 3
- To solve this, first of all, we have to write this in the form of a Matrix. I have solved the example in Page, and all the details have been mentioned on a page by me.

Solving Linear Equations on Paper. |
|---|

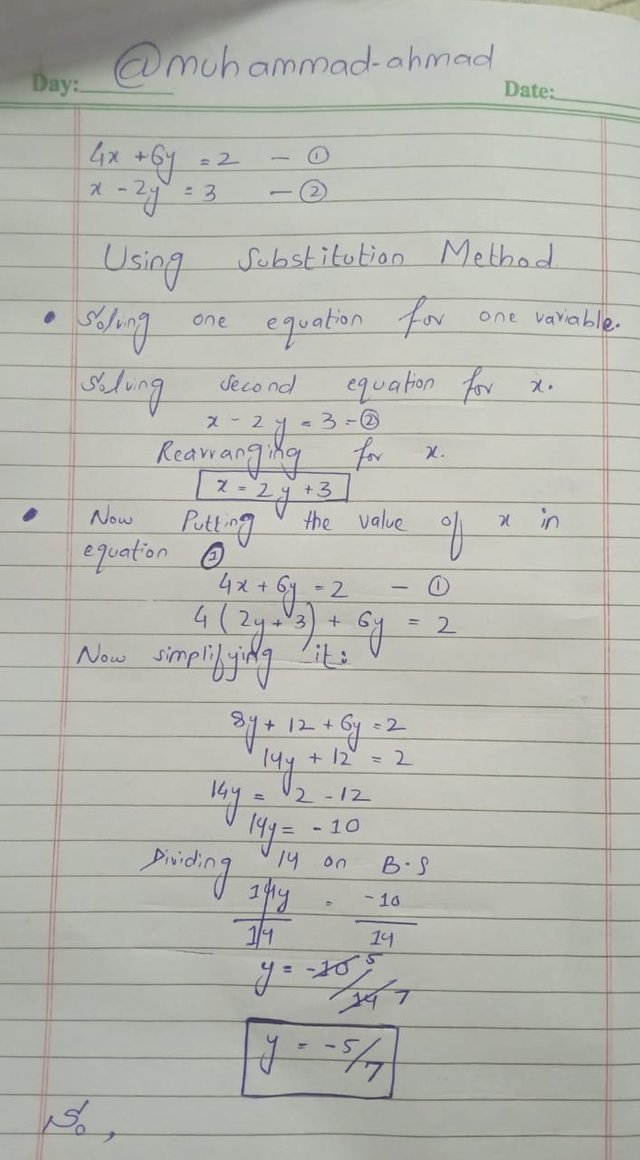

Solving Scenario 1 given to us by our instructor. |
|---|
Scenario: 1
Solving this scenario for y (units of product B), given that x is equal to 50. (units of product A) According to the Equation in the scenario.
- Cost of Materials :- 2x+3y = 130
- Cost of Labor :- x+2y = 110
In these 2 equations, now we have to put 50 in place of x. Like we are substituting the value of x by 50.So,
2x+3y=130
when x = 50 then.
- 2(50)+3y = 130
Multiplying 50 by 2 we get 100. - 100+3y = 130
Shifting 100 on the other side. - 3y = 130−100
Subtracting 130 from 100. - 3y = 30
Dividing 3 on both sides. - y = 30/3
Dividing 30 on 3. - y = 10
x+2y=110
when x = 50 then.
- 50+2y = 110
Shifting 50 on the other side. - 2y = 110−50
Subtracting 110 from 50. - 2y = 60
Dividing 2 on both sides. - y = 60/2
Dividing 60 on 2. - y = 30.
Solving Scenario 2 given to us by our instructor. |
|---|
Scenario: 2
We have to calculate y (No of chocolate cakes) as x = 30 is given ( (No of vanilla cakes). Equations are:
Cost of Ingredients:- x+2y = 80
Cost of Labor:- 2x+y = 70
In these 2 equations, now we have to put 30 in place of x. Like we are substituting the value of x by 30.So,
x+2y = 80
when x = 30 then.
- 30+2y = 80
Shifting 30 on the other side. - 2y = 80−30
Subtracting 80 from 30. - 2y = 50
Subtracting 2 on both sides. - y = 50/2
Dividing 50 by 2. - y = 25.
2x+y = 70
when x = 30 then.
- 2(30)+y = 70
Multiplying 2 with 30. - 60+y=70
Shifting 60 on the other side. - y = 70−60
Subtracting 70 from 60, we get. - y = 10.
- I would like to invite Dear. @kouba01, Dear. @suboohi, and Dear. @goodybest to participate in this. Once again Thank you so much. I am highly obliged.
.png)