The History of Music: Pythagoras' Theory of Music
In the previous episode, I talked about the oldest known music in history, including the earliest complete composition found on a tombstone about a man lamenting the death of his wife 2,000 years ago, 'The Seikilos Epitaph'.
Although this music was by no means the earliest written music - Numerous sources go back millennia or earlier than the Greeks - this is the earliest complete piece. However, all this historical music succumbs to the same general problems when it comes to writing things down: There was a lack of detail. The most persistent problem seemed to be a lack of any reference point. What is C? where does one begin? How large is the space between one note and another?

Not helpful... Public Domain
All music of the past was either passed down by memory or written as vague wiggles and signs to show a general, intuitive direction for the voice to go. There wasn't even any way to notate rhythm.
So, to get to something at least familiar with whaat we know and love today:

Public Domain
We have a long, arduous... I mean, fascinating journey to travel. We're going to start 2,500 years ago and we're going to see some fundamental awesomeness on the way.
Pythagoras' Theory of Music
Around 500BC, Pythagoras, after messing around with a bunch of triangles or whatever, decided to turn his interest to music. At this time, strangely, music was considered as part of the sciences, and well, it does involve a lot of math, as Pythagoras was quick to realize.
He decided that pitches of notation can be determined using equally divided ratios, making it much easier to standardize the intervals between a given note and another. This is harder than it sounds.
For example, from C to E is a third interval (C, D, E = 3 notes), and an E to G is also a third interval. But how can we be sure the distance between C and E, and E and G, are identical? And how do we know that G to C is going to return us to the same pitch as the first C, without going out of tune a little?
Thankfully, the Universe works in mysterious, aka mathematical, ways, and Pythagoras figured out that things can all fit together in more or less equally divisble spaces.
How it all worked out
Pythagoras noted that when you pluck a string, it wobbles at a certain frequency, measured now in Hertz (Hz). When a string wobbles 110 times per second, it has a frequency of 110Hz - an A note (see below). If you suddenly half the length of that string with a finger, the string will double its wobbling speed to 220Hz - 220 wobbles per second, another A. Or fret 12 on a guitar's A string.
If you half that distance again - fret 24 on a guitar - you get 440Hz, an even higher A. And so on. These are Octaves and have a ratio of 2:1; if one string wobbles at 110Hz and a second at 220Hz, then the second string wobbles twice as fast as the other.
However, there are many more ratios, depending on how you divide up the string. It just so happens that if you put your finger down 2/3rds of the way down a string, you get a ratio of 3:2; for every 2 wobbles with the open string, you get 3 wobbles during the same period once the finger is put down.
I thought this might seem complicated to visualize from my terrible communication skills so I thought I'd demonstrate using my phone's slow-motion feature.
The Experiment
This was a hell of a lot of fun for me to do. First, I had to tune my guitar way down, to the point that the lowest string was barely audible and pretty difficult to hear what pitch it was resonating at. Then I tuned the second string a 5th higher, which should demonstrate the 3:2 ratio. Finally, the third string was tuned an octave above the first string to demonstrate the 2:1 ratio.
I recorded at 480fps, then halved the speed again in editing to 960 frames per second. That number is important. Follow my finger carefully while keeping the lowest, slowest string in your peripheral vision. You'll get it!
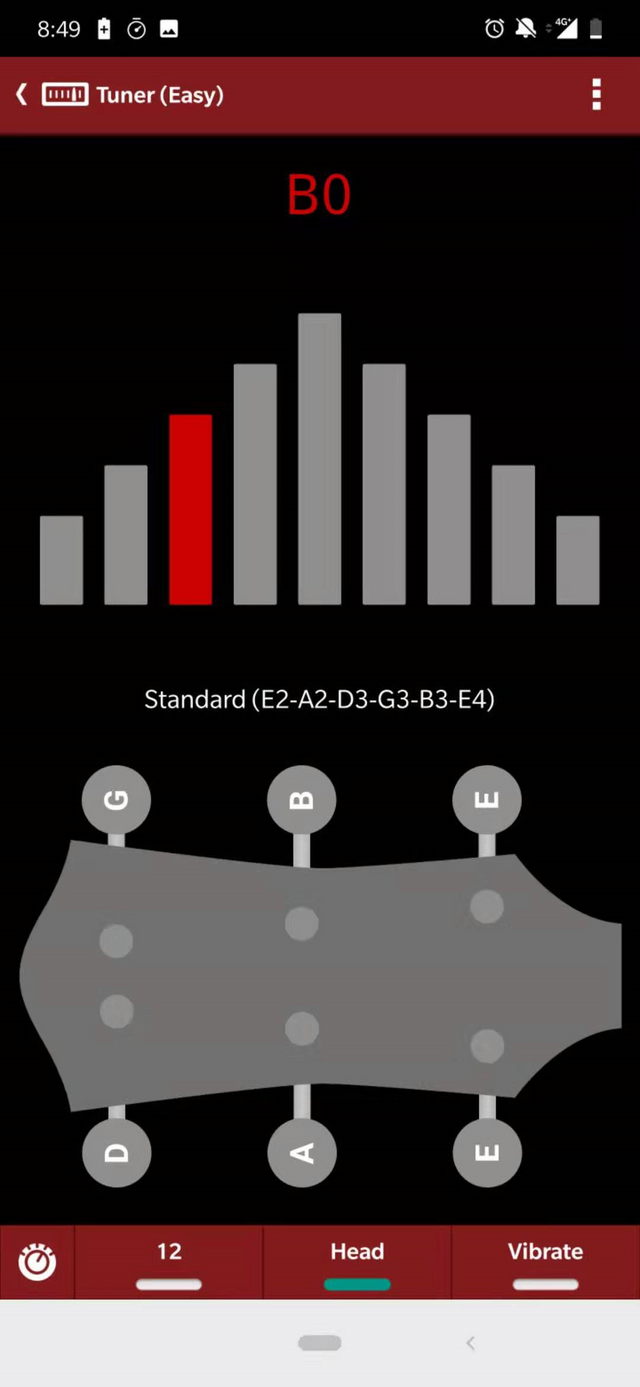
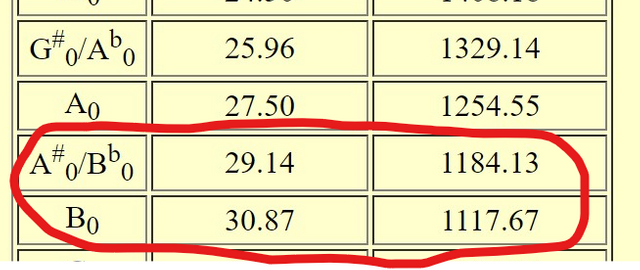
Now here comes the magic. I got my guitar tuner to figure out exactly what note was being played. The lowest string turned out to be a little lower than B, somewhere between B and B-flat:
A guitar tuner works by measuring the frequency of peaks and troughs of a sound wave, thus determining the length of that wave. If we are somewhere between B and B-flat, this sound wave should be about 1,150cm According to the chart below:
Next, I put on a metronome and timed the lowest string to see how many times it wobbled per second in the video - around 109 times per minute - 1.8 times per second. But, we have to remember we're at 960 frames per second and we need to speed things back up to real-time. The video playback was about 29.6 frames per second in real-time.
So, we can divide 960 by 29.6 and find the footage needs to be 32-ish times faster.
Thus, 1.8 x 32.4 = 58.3 wobbles per second in real-time, or 58.3Hz.
Right in between B and B-flat!

Note, as the string was tuned so exceptionally low, it becomes very loose and floppy, so the pitch varies quite broadly between the time you strike the string (higher) and the following seconds (lower).
I should also note that this frequency of the B is an octave higher than my tuner stated, so I probably didn't multiply a number enough or something. I'm not a mathematician. Any of you out there who can bring some light on this, I welcome it in the comments.
The point is...
...that Pythagoras realized these ratios between pitches and created a tuning system based on the 5th interval, the interval he considered the purest.
Let's start at the pitch C. Now, using the 3:2 ratio by cutting the length of a string by 2/3rds, you get a fifth interval higher - G:
As you can see, you can go from G and continue around another 3:2 ratio and get the next fifth - D. Follow this round to A, E, B and finally F. Jumping another 3:2 from F brings you precisely back to C (F, G, A, B, C - 1, 2, 3, 4, 5) and you have now a consistent, measurable way to determine the pitch of music!
And all you need is a piece of string.
This ancient 'Pythagorean tuning' is surprisingly accurate when compared to the modern 'equal temperament', with only subtle differences:
And some musicians still use this ancient system to this day.
However
After all this, and for centuries after... there is still no explanation for, say, What is C?
If a church in one location sang a hymn written in a book, you can guarantee the church down the road will sing it totally differently even if, thanks to Pythagoras, the space between notes is now standard. And what about rhythm? How on earth are we going to solve these dilemmas?
Next time!
Sources: Pythagorean Tuning | The overtone series | vpr.org


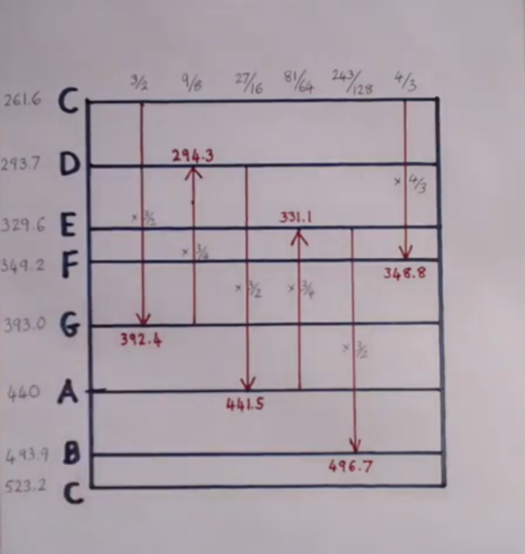
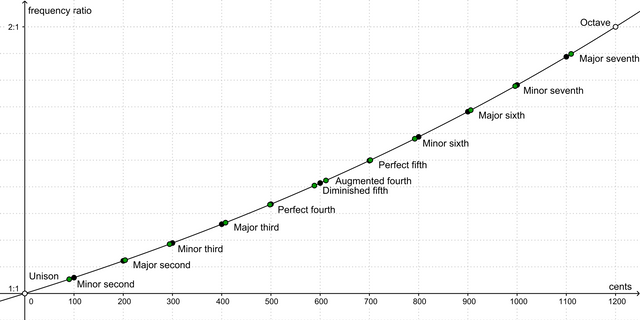
Your piece sent me off to second and third sources to explore tangential questions that occurred to me. I'm probably way off base, but as I read about the symmetry of spaces between notes, I thought of something @lemouth described: the law of symmetry in physics. It seems that music corresponds to the same principle. Or at least, it seems that way.
I found a few articles, this one the easiest (for me) to understand. As I read, I realize that, while there is certainty about specific principles and laws, there is also uncertainty.
A fascinating piece. Even if my questions lead me astray, I'm learning as I go:)
You know you're going down the rabbit hole when you're reading from sites that look like they're from the '90s =P
But it's awesome that I was the cause of digging deeper, I found this super difficult to explain what I feel is a fairly simple idea, but in terms anyone can understand without any knowledge of music at all. I guess its always a challenge to communicate a profession in a way a child can understand... Need practice!
(Not that you know nothing, but just generally for everyone)
As for uncertainty, well, it's actually technically impossible for these frequencies to match perfectly as I imply above, for reasons of physics I'll get to in a much later post, but that whole area is pretty fascinating
I'm always modest in my expectations. And open. There's no downside to experience, here or elsewhere, that way.
The music of the elementary particles? :)
Sounds beautiful to me 🎼 😇
cant follow up lately but i just bumped into something, made me think id drop it here in case of interested or inspirational (and sadly have to get to the answering later, i think i'm closing in on 18 days behind, sorry for the chaos ... as always)
You're not obliged to comment! lol
quite impressive singing and performing there, do you know in which language it is? I listened almost to the end. Good night :)
Hello!
This post has been manually curated, resteemed
and gifted with some virtually delicious cake
from the @helpiecake curation team!
Much love to you from all of us at @helpie!
Keep up the great work!
Manually curated by @georgeboya.
@helpie is a Community Witness.
For more information about our project,
please visit this month’s UPDATE post.
This post was shared in the Curation Collective Discord community for curators, and upvoted and resteemed by the @c-squared community account after manual review.
@c-squared runs a community witness. Please consider using one of your witness votes on us here
The answer to the question (what is C) sounds as unknown as why the basic ratios were considered as pure by the Greeks (and those ratios seem to pervade the current system).